题目内容
根据下列条件,写出直线的方程,并把它化成一般式:
(1)经过点A(8,-2),斜率是-
;
(2)经过点B(4,2),平行于x轴;
(3)经过点P1(3,-2),P2(5,-4);
(4)在x轴、y轴上的截距分别是
,-3.
(1)经过点A(8,-2),斜率是-
| 1 |
| 2 |
(2)经过点B(4,2),平行于x轴;
(3)经过点P1(3,-2),P2(5,-4);
(4)在x轴、y轴上的截距分别是
| 3 |
| 2 |
考点:直线的一般式方程
专题:直线与圆
分析:(1)由点斜式即可得出;
(2)由已知可得方程y=2;
(3)由两点式即可得出;
(4)利用截距式即可得出.
(2)由已知可得方程y=2;
(3)由两点式即可得出;
(4)利用截距式即可得出.
解答:
解:(1)由点斜式可得y+2=-
(x-8),化为x+2y-4=0;
(2)∵经过点B(4,2),平行于x轴,可得方程y=2;
(3)由两点式可得:
=
,化为一般式x+y-1=0;
(4)在x轴、y轴上的截距分别是
,-3,可得
+
=1,化为2x-y-3=0.
| 1 |
| 2 |
(2)∵经过点B(4,2),平行于x轴,可得方程y=2;
(3)由两点式可得:
| y-(-2) |
| -4-(-2) |
| x-3 |
| 5-3 |
(4)在x轴、y轴上的截距分别是
| 3 |
| 2 |
| x | ||
|
| y |
| -3 |
点评:本题考查了直线方程的各种形式及其一般式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
已知实数x、y满足
,若z=x-y的最大值为1,则实数b的取值范围是( )
|
| A、b≥1 | B、b≤1 |
| C、b≥-1 | D、b≤-1 |
设{an}是等差数列,若log2a7=3,则a6+a8等于( )
| A、6 | B、8 | C、9 | D、16 |
定义在R上的奇函数f(x)在[-1,0]上单调递减,则下列关系式正确的是( )
| A、0<f(1)<f(-1) |
| B、f(-1)<f(1)<0 |
| C、f(-1)<0<f(1) |
| D、f(1)<0<f(-1) |
设P(x,2)为角α终边上的一点,且sinα=
,则tanα=( )
| ||
| x |
| A、1 | B、-1 | C、±1 | D、±2 |
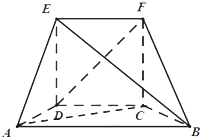 如图,几何体EF-ABCD中,CDEF为边长为2的正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,AD=2,AB=4,∠ADF=90°.
如图,几何体EF-ABCD中,CDEF为边长为2的正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,AD=2,AB=4,∠ADF=90°.