题目内容
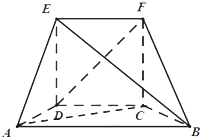如图，几何体EF-ABCD中，CDEF为边长为2的正方形，ABCD为直角梯形，AB∥CD，AD⊥DC，AD=2，AB=4，∠ADF=90°．（1）求证：AC⊥FB
（2）求几何体EF-ABCD的体积．
考点：棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题：空间位置关系与距离
分析：（1）证明AD⊥FC，然后证明FC⊥平面ABCD，推出AC⊥平面FCB，利用直线与平面垂直的性质定理证明AC⊥FB；
（2）利用几何体的体积V=VE-ABCD+VB-CEF，分别求得两个棱锥的底面面积与高，代入棱锥的体积公式计算．
（2）利用几何体的体积V=VE-ABCD+VB-CEF，分别求得两个棱锥的底面面积与高，代入棱锥的体积公式计算．
解答：
解：（1）证明：由题意得，AD⊥DC，AD⊥DF，且DC∩DF=D，
∴AD⊥平面CDEF，∴AD⊥FC，…2分
∵四边形CDEF为正方形．∴DC⊥FC
由DC∩AD=D，∴FC⊥平面ABCD
∴FC⊥AC…4分
又∵四边形ABCD为直角梯形，AB∥CD，AD⊥DC，AD=2，AB=4
∴AC=2
，BC=2
则有AC2+BC2=AB2
∴AC⊥BC
由BC∩FC=C，∴AC⊥平面FCB，
∴AC⊥FB…6分
（2）连结EC，过B作CD的垂线，垂足为N，
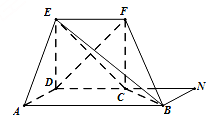
易见BN⊥平面CDEF，且BN=2．…8分
∵VEF-ABCD=VE-ABCD+VB-ECF…9分
=
S△ABCD•DE+
S△EFC•BN=
…11分
∴几何体EF-ABCD的体积为
…12分
∴AD⊥平面CDEF，∴AD⊥FC，…2分
∵四边形CDEF为正方形．∴DC⊥FC
由DC∩AD=D，∴FC⊥平面ABCD
∴FC⊥AC…4分
又∵四边形ABCD为直角梯形，AB∥CD，AD⊥DC，AD=2，AB=4
∴AC=2
| 2 |
| 2 |
∴AC⊥BC
由BC∩FC=C，∴AC⊥平面FCB，
∴AC⊥FB…6分
（2）连结EC，过B作CD的垂线，垂足为N，
易见BN⊥平面CDEF，且BN=2．…8分
∵VEF-ABCD=VE-ABCD+VB-ECF…9分
=
| 1 |
| 3 |
| 1 |
| 3 |
| 16 |
| 3 |
∴几何体EF-ABCD的体积为
| 16 |
| 3 |
点评：本题考查棱柱、棱锥、棱台的体积，直线与直线的垂直，直线与平面垂直的性质定理的应用，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
设集合A={x∈Q|x＞-1}，则（ ）
| A、∅∉A | ||
B、
| ||
| C、{2}?A | ||
D、{
|
从2011名学生中选取50名组成参观团，若采用下面的方法选取，先用简单随机抽样法从2011人中剔除11人，剩下的2000人再按系统抽样的方法进行，则每人入选的概率（ ）
| A、不全相等 | ||
| B、均不相等 | ||
C、都相等且为
| ||
D、都相等且为
|
已知A={1，2，5}，B={2，3，5}，则A∪B等于（ ）
| A、{2，3} |
| B、{2，5} |
| C、{2} |
| D、{1，2，3，5} |