题目内容
16.当a取不同实数时,直线(2+a)x+(a-1)y+3a=0恒过一个定点,这个定点的坐标为(-1,-2).分析 根据直线(a+2)x+(a-1)y+3a=0可变为a(x+y+3)+2x-y=0,令x+y+3=0、2x-y=0可得答案.
解答 解:∵(a+2)x+(a-1)y+3a=0,
∴a(x+y+3)+2x-y=0
令x+y+3=0、2x-y=0
解得:x=-1,y=-2
∴恒过点(-1,-2)
故答案为:(-1,-2).
点评 本题主要考查含参数的直线方程恒过定点的问题.这里要分离出参数进而求解.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
7.非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{b}$|=2,<$\overrightarrow{a}$,$\overrightarrow{b}$>=30°,且对?λ>0,且|$\overrightarrow{a}$-λ$\overrightarrow{b}$|≥|$\overrightarrow{a}$-$\overrightarrow{b}$|恒成立,则$\overrightarrow{a}$•$\overrightarrow{b}$=( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
6.已知命题p:$\frac{1}{x-1}$<1,q:x2+(a-1)x-a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
| A. | (-2,-1] | B. | [-2,-1] | C. | [-3,-1] | D. | [-2,+∞) |
3.已知i是虚数单位,则复数z=$\frac{4+3i}{1+2i}$的虚部为( )
| A. | -i | B. | 11 | C. | 1 | D. | -1 |
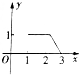
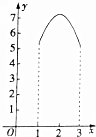
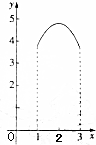
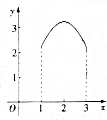
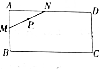 如图,矩形ABCD的周长为8,设AB=x(1≤x≤3),线段MN的两端点在矩形的边上滑动,且MN=1,当N沿A→D→C→B→A在矩形的边上滑动一周时,线段MN的中点P所形成的轨迹为G,记G围成的区域的面积为y,则函数y=f(x)的图象大致为( )
如图,矩形ABCD的周长为8,设AB=x(1≤x≤3),线段MN的两端点在矩形的边上滑动,且MN=1,当N沿A→D→C→B→A在矩形的边上滑动一周时,线段MN的中点P所形成的轨迹为G,记G围成的区域的面积为y,则函数y=f(x)的图象大致为( )