题目内容
14．复数z=$\frac{5}{i+2}$在复平面内，z所对应的点在第四象限．分析 直接利用复数代数形式的乘法运算化简，然后求得点的坐标．
解答 解：z=$\frac{5}{i+2}$=$\frac{5（2-i）}{（2+i）（2-i）}$=2-i，
z在复平面内对应点的坐标是（2，-1），
故z所对应的点在第四象限，
故答案为：四．
点评 本题考查了复数代数形式的乘法运算，考查了复数的代数表示法及其几何意义，是基础题．
练习册系列答案
新思维寒假作业系列答案
相关题目
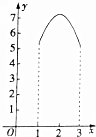
5．二次函数f（x）的图象如图所示，则f（x-1）＞0的解集为（ ）
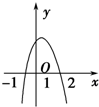
| A． | （-2，1） | B． | （0，3） | C． | （-1，2] | D． | （-∞，0）∪（3，+∞） |
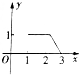
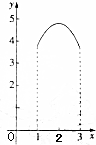
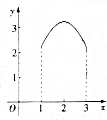
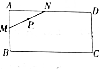如图，矩形ABCD的周长为8，设AB=x（1≤x≤3），线段MN的两端点在矩形的边上滑动，且MN=1，当N沿A→D→C→B→A在矩形的边上滑动一周时，线段MN的中点P所形成的轨迹为G，记G围成的区域的面积为y，则函数y=f（x）的图象大致为（ ）
3．袋中有2个红色的变形金刚，2个白色的变形金刚，2个黑色的变形金刚，从里面任意取2个变形金刚，不是基本事件的为（ ）
| A． | {恰好2个红色的变形金刚} | B． | {恰好2个黑色的变形金刚} | ||
| C． | {恰好2个白色的变形金刚} | D． | {至少1个红色的变形金刚} |