题目内容
19．已知函数f（x）=sin2x-kcos2x的图象关于直线x=$\frac{π}{8}$对称，则k的值是-1．分析 由对称性可得f（0）=f（$\frac{π}{4}$），代值解方程可得．
解答 解：∵函数f（x）=sin2x-kcos2x的图象关于直线x=$\frac{π}{8}$对称，
∴f（0）=f（$\frac{π}{4}$），即-k=1，可得k=-1，
故答案为：-1．
点评 本题考查三角函数图象的对称性，属基础题．
练习册系列答案
相关题目
9．等比数列{an}中，a1•a7=4，则a22+a62的最小值为（ ）
| A． | 4 | B． | 6 | C． | 8 | D． | 10 |
7．已知集合A={-1，0，1}，B={x|y=x2，x∈R}，则A∩B=（ ）
| A． | {0，1} | B． | {-1，0，1} | C． | {1} | D． | ∅ |
14．从甲、乙两品种的棉花中各抽测了10根棉花的纤维长度（单位：mm），所得数据如图茎叶图．记甲、乙两品种棉花的纤维长度的平均值分别为$\overline{{x}_{甲}}$，$\overline{{x}_{乙}}$，标准差分别为s甲，s乙，则（ ）
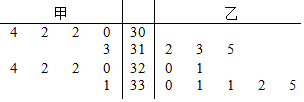
| A． | $\overline{{x}_{甲}}$＜$\overline{{x}_{乙}}$，s甲＞s乙 | B． | $\overline{{x}_{甲}}$＜$\overline{{x}_{乙}}$，s甲＜s乙 | ||
| C． | $\overline{{x}_{甲}}$＞$\overline{{x}_{乙}}$，s甲＞s乙 | D． | $\overline{{x}_{甲}}$＞$\overline{{x}_{乙}}$，s甲＜s乙 |
4．如图所示的程序框图的运行结果为（ ）
| A． | -1 | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
11．
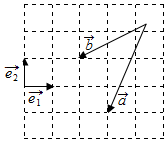如图，设$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$为互相垂直的单位向量，则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为（ ）
如图，设$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$为互相垂直的单位向量，则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为（ ）| A． | 2$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$ | B． | 3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | C． | 2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ | D． | $\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ |