题目内容
已知函数f(x)=2lnx-
ax2-3x,其中a为常数.若当x=1时,f(x)取得极值,求a的值,并求出f(x)的单调区间.
| 1 |
| 2 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:先求出函数的定义域,函数有极值,则其导数等于0,先求导,代入求出a的值,再根据导数和函数的单调性的关系,求出单调区间.
解答:
解:f(x)=2lnx-
ax2-3x的定义域为(0,+∞)
∵f′(x)=
-ax-3,
∵当x=1时,f(x)取得极值,
∴f′(1)=0,
即2-a-3=0,
解得a=-1,
∴f′(x)=
+x-3=
=
,
令f′(x)=0,解得x=1,或x=2,
当f′(x)>0时,解得0<x<1,或x>2,
当f′(x)<0时,解得1<x<2,
故函数f(x)在(0,1)和(2,+∞)上为增函数,在(1,2)上为减函数
| 1 |
| 2 |
∵f′(x)=
| 2 |
| x |
∵当x=1时,f(x)取得极值,
∴f′(1)=0,
即2-a-3=0,
解得a=-1,
∴f′(x)=
| 2 |
| x |
| x2-3x+2 |
| x |
| (x-1)(x-2) |
| x |
令f′(x)=0,解得x=1,或x=2,
当f′(x)>0时,解得0<x<1,或x>2,
当f′(x)<0时,解得1<x<2,
故函数f(x)在(0,1)和(2,+∞)上为增函数,在(1,2)上为减函数
点评:本题考查了导数和函数的单调性极值的关系,需要注意不要忘了对数函数的定义域,属于中档题

练习册系列答案
相关题目
若函数f(x)=xcosx在(0,+∞)内的全部极值点按从小到大的顺序排列为a1,a2,…,an,…,则对任意正整数n必有( )
A、π<an+1-an<
| ||
B、
| ||
C、0<an+1-an<
| ||
D、-
|
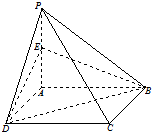 如图:在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E为PA中点.
如图:在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E为PA中点. 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行,数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…,以此类推,则第11行从左至右算第7个数字为
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行,数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…,以此类推,则第11行从左至右算第7个数字为 如图,在正三棱柱ABC-A1B1C1中,若各条棱长均为2,且M为A1C1的中点,则三棱锥M-AB1C的体积是
如图,在正三棱柱ABC-A1B1C1中,若各条棱长均为2,且M为A1C1的中点,则三棱锥M-AB1C的体积是