题目内容
17.已知函数f(x)是定义在R上的奇函数,f(3)=2,且对于一切实数x,都有f(x+4)=f(x),则f(13)=-2.分析 根据题意,由f(x+4)=f(x),可得函数f(x)的周期为4,进而可得f(13)=f(-3),又由函数f(x)为奇函数,则有f(-3)=-f(3),联立可得f(13)=-2,即可得答案.
解答 解:根据题意,由f(x+4)=f(x),可得函数f(x)的周期为4,
故f(13)=f(-3+4×4)=f(-3),
又由函数f(x)为奇函数,则f(-3)=-f(3)=-2,
综合可得f(13)=f(-3)=-2,
故答案为:-2.
点评 本题考查函数的奇偶性与周期性的综合运用,关键是由f(x+4)=f(x)分析出函数的周期.

练习册系列答案
相关题目
7.在四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{DC}$=($\sqrt{2}$,$\sqrt{2}$),$\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|}$+$\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}$=$\sqrt{3}$$\frac{\overrightarrow{BD}}{|\overrightarrow{BD}|}$,则四边形ABCD的面积为( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
8.将函数y=sin(2x-$\frac{π}{6}$)的图象向左平移$\frac{π}{3}$个单位,再将得到的图象上的点的横坐标伸长到原来的2倍(纵坐标不变)后得到的函数y=g(x)的图象.若方程g(x)-a=0,x∈($\frac{π}{2}$,3π)有三个根,且这三根可以构成等比数列,则实数a的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{1}{2}$ |
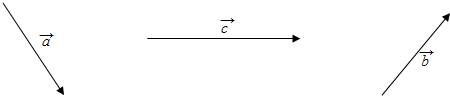
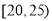 ,第2组
,第2组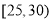 ,第3组
,第3组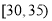 ,第4组
,第4组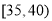 ,第5组
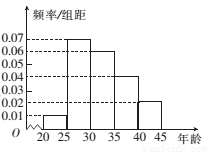
,第5组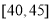 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.