题目内容
14.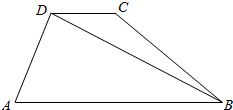 如图,在梯形ABCD中,已知AB∥CD,∠A=60°,∠ABC=45°,AD=3cm,AB=5cm,求:BC、CD、BD.
如图,在梯形ABCD中,已知AB∥CD,∠A=60°,∠ABC=45°,AD=3cm,AB=5cm,求:BC、CD、BD.
分析 过D作DE⊥AB于E,过C作CF⊥AB于F,利用特殊角的三角函数值,即可得出结论.
解答 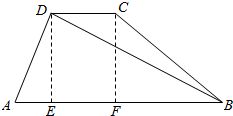 解:过D作DE⊥AB于E,过C作CF⊥AB于F.
解:过D作DE⊥AB于E,过C作CF⊥AB于F.
∵AD=3,∠DAB=60°,
∴AE=$\frac{3}{2}$,ED=$\frac{3\sqrt{3}}{2}$=CF,
∵∠ABC=45°,AB=5cm,
∴BE=$\frac{7}{2}$,BF=CF=$\frac{3\sqrt{3}}{2}$,
∴BC=$\sqrt{2}$CF=$\frac{3\sqrt{6}}{2}$,
CD=EF=BE-BF=$\frac{7-3\sqrt{3}}{2}$,BD=$\sqrt{B{E}^{2}+D{E}^{2}}$=$\sqrt{19}$.
点评 本题考查三角形中线段长的求解,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
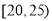 ,第2组
,第2组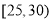 ,第3组
,第3组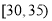 ,第4组
,第4组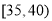 ,第5组
,第5组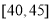 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.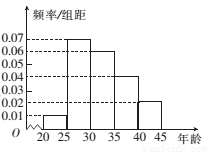
 ,则下列关系式错误的是( )
,则下列关系式错误的是( ) B.
B. C.
C. D.
D.