题目内容
13.已知复数z1=(1+i)(2i-1)和复数z2=m+$\frac{2×{i}^{2015}}{1-i}$,当m=-4时,z1=$\overline{{z}_{2}}$.分析 化简复数z1与z2,利用z1=$\overline{{z}_{2}}$列出方程求出m的值.
解答 解:∵复数z1=(1+i)(2i-1)=-3+i,
复数z2=m+$\frac{2×{i}^{2015}}{1-i}$=m+$\frac{-2i(1+i)}{1{-i}^{2}}$=(m+1)-i,
∴$\overline{{z}_{2}}$=(m+1)+i;
又z1=$\overline{{z}_{2}}$,
∴m+1=-3,解得m=-4;
∴当m=-4时,z1=$\overline{{z}_{2}}$.
故答案为:-4.
点评 本题考查了复数的概念与代数运算问题,也考查了转化思想与解方程的应用问题,是基础题目.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
8.将函数y=sin(2x-$\frac{π}{6}$)的图象向左平移$\frac{π}{3}$个单位,再将得到的图象上的点的横坐标伸长到原来的2倍(纵坐标不变)后得到的函数y=g(x)的图象.若方程g(x)-a=0,x∈($\frac{π}{2}$,3π)有三个根,且这三根可以构成等比数列,则实数a的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{1}{2}$ |
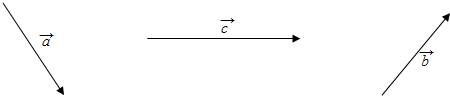
 ,则下列关系式错误的是( )
,则下列关系式错误的是( ) B.
B. C.
C. D.
D.