题目内容
10.为加强大学生实践、创新能力和团队精神的培养,促进高等教育教学改革,教育部门主办了全国大学生智能汽车竞赛.该竞赛分为预赛和决赛两个阶段.通过预赛,选拔出甲、乙等五支队伍参加决赛,参加决赛的队伍按照抽签方式决定出场顺序.(Ⅰ)求决赛中甲、乙两支队伍恰好排在前两位的概率;
(Ⅱ) 若决赛中甲队和乙队之间间隔的队伍数记为X,求X的分布列和数学期望E(X).
分析 (Ⅰ)决赛中甲、乙两支队伍恰好排在前两位可有两种排法,其余3支队伍共有3!种排法,利用乘法原理,即可求得结论;
(Ⅱ)确定x的可能取值,求出概率,即可得到分辨率与期望.
解答 (Ⅰ)解:(Ⅰ)设“甲、乙两支队伍恰好排在前两位”为事件A,则P(A)=$\frac{2{×A}_{3}^{3}}{{A}_{5}^{5}}=\frac{1}{10}$
所以 甲、乙两支队伍恰好排在前两位的概率为$P=\frac{1}{10}$…..(5分)
(Ⅱ)(Ⅱ)随机变量X的可能取值为0,1,2,3(6分)
P(X=0)=$\frac{2×4!}{5!}=\frac{2}{5}$,P(X=1)=$\frac{3×2×3!}{5!}=\frac{3}{10}$,P(X=2)=$\frac{2×2!×3×2!}{5!}=\frac{1}{5}$,P(X=3)=$\frac{1}{10}$.
所以X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{1}{5}$ | $\frac{1}{10}$ |
点评 本题考查概率的求解,考查分布列与期望,解题的关键是确定变量的取值与含义,正确计算其概率,属于基础题.

练习册系列答案
相关题目
7.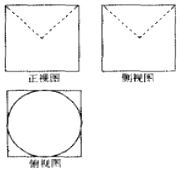 某几何体的三视图如图所示,图中四边形都是边长为2的正方形,两条虚线相互垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中四边形都是边长为2的正方形,两条虚线相互垂直,则该几何体的表面积是( )
 某几何体的三视图如图所示,图中四边形都是边长为2的正方形,两条虚线相互垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中四边形都是边长为2的正方形,两条虚线相互垂直,则该几何体的表面积是( )| A. | $24+({\sqrt{2}+1})π$ | B. | $24+({\sqrt{2}-1})π$ | C. | $24-({\sqrt{2}+1})π$ | D. | $24-({\sqrt{2}-1})π$ |
1.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的焦点为F1,F2,且C上的点P满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=0,|PF1|=3,|PF2|=4,则双曲线C的离心率为( )
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{5}{2}$ | D. | 5 |