题目内容
19.函数fn(x)=xn+bx+c(n∈Z,b,c∈R).(1)若n=-1,且f-1(1)=f-1($\frac{1}{2}$)=4,试求实数b,c的值;
(2)设n=2,若对任意x1,x2∈[-1,1]有|f2(x1)-f2(x2)|≤4恒成立,求b的取值范围;
(3)当n=1时,已知bx2+cx-a=0,设g(x)=$\frac{{\sqrt{1-{x^4}}}}{{1+{x^2}}}$,是否存在正数a,使得对于区间$[{-\frac{{2\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5}}]$上的任意三个实数m,n,p,都存在以f1(g(m)),f1(g(n)),f1(g(p))为边长的三角形?若存在,求出a的取值范围;若不存在,请说明理由.
分析 (1)由条件,可得b,c的方程,解方程可得b,c;
(2)当n=2时,f2(x)=x2+bx+c,对任意x1,x2∈[-1,1]有|f2(x1)-f2(x2)|≤4恒成立等价于f2(x)在[-1,1]上的最大值与最小值之差M≤4.讨论对称轴和区间的关系,判断单调性,可得最值,解不等式即可得到所求范围;
(3)设t=g(x)=$\frac{{\sqrt{1-{x^4}}}}{{1+{x^2}}}$=$\sqrt{\frac{1-{x}^{2}}{1+{x}^{2}}}$=$\sqrt{\frac{2}{1+{x}^{2}}-1}$,由x∈$[{-\frac{{2\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5}}]$,可得t∈[$\frac{1}{3}$,1].则y=t+$\frac{a}{t}$在[$\frac{1}{3}$,1]上恒有2ymin>ymax.讨论顶点处x=$\sqrt{a}$与区间[$\frac{1}{3}$,1]的关系,求得单调性,可得最值,解不等式即可得到存在,求得a的范围.
解答 解:(1)n=-1,且${f_{-1}}(1)={f_{-1}}({\frac{1}{2}})=4$,
可得1+b+c=4,2+$\frac{1}{2}$b+c=4,解得b=2,c=1;
(2)当n=2时,f2(x)=x2+bx+c,
对任意x1,x2∈[-1,1]有|f2(x1)-f2(x2)|≤4恒成立等价于
f2(x)在[-1,1]上的最大值与最小值之差M≤4.
①当-$\frac{b}{2}$<-1,即b>2时,f2(x)在[-1,1]递增,
f2(x)min=f2(-1)=1-b+c,f2(x)max=f2(1)=1+b+c,
M=2b>4(舍去);
②当-1≤-$\frac{b}{2}$≤0,即0≤b≤2时,f2(x)在[-1,-$\frac{b}{2}$]递减,在(-$\frac{b}{2}$,1]递增,
f2(x)min=f2(-$\frac{b}{2}$)=c-$\frac{{b}^{2}}{4}$,f2(x)max=f2(1)=1+b+c,M=($\frac{b}{2}$+1)2≤4恒成立,故0≤b≤2;
③当0<-$\frac{b}{2}$≤1即-2≤b<0时,f2(x)在[-1,-$\frac{b}{2}$]递减,在(-$\frac{b}{2}$,1]递增,
f2(x)min=f2(-$\frac{b}{2}$)=c-$\frac{{b}^{2}}{4}$,f2(x)max=f2(-1)=1-b+c,M=($\frac{b}{2}$-1)2≤4恒成立,故-2≤b<0;
④当-$\frac{b}{2}$>1,即b<-2时,f2(x)在[-1,1]递减,
f2(x)min=f2(1)=1+b+c,f2(x)max=f2(-1)=1-b+c,
M=-2b>4矛盾.
综上可得,b的取值范围是-2≤b≤2;
(3)设t=g(x)=$\frac{{\sqrt{1-{x^4}}}}{{1+{x^2}}}$=$\sqrt{\frac{1-{x}^{2}}{1+{x}^{2}}}$=$\sqrt{\frac{2}{1+{x}^{2}}-1}$,
由x∈$[{-\frac{{2\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5}}]$,可得t∈[$\frac{1}{3}$,1].
则y=t+$\frac{a}{t}$在[$\frac{1}{3}$,1]上恒有2ymin>ymax.
①当a∈(0,$\frac{1}{9}$]时,y=t+$\frac{a}{t}$在[$\frac{1}{3}$,1]上递增,
ymin=$\frac{1}{3}$+3a,ymax=a+1,又2ymin>ymax.
则a>$\frac{1}{15}$,即有$\frac{1}{15}$<a≤$\frac{1}{9}$;
②当a∈($\frac{1}{9}$,$\frac{1}{3}$]时,y=t+$\frac{a}{t}$在[$\frac{1}{3}$,$\sqrt{a}$)递减,($\sqrt{a}$,1)递增,
可得ymin=2$\sqrt{a}$,ymax=max{3a+$\frac{1}{3}$,a+1}=a+1,又2ymin>ymax.
解得7-4$\sqrt{3}$<a<7+4$\sqrt{3}$,即有$\frac{1}{9}$<a≤$\frac{1}{3}$;
③当a∈($\frac{1}{3}$,1)时,y=t+$\frac{a}{t}$在[$\frac{1}{3}$,$\sqrt{a}$)递减,($\sqrt{a}$,1)递增,
可得ymin=2$\sqrt{a}$,ymax=max{3a+$\frac{1}{3}$,a+1}=3a+$\frac{1}{3}$,又2ymin>ymax.
解得$\frac{7-4\sqrt{3}}{9}$<a<$\frac{7+4\sqrt{3}}{9}$,即有$\frac{1}{3}$<a<1;
④当a∈[1,+∞)时,y=t+$\frac{a}{t}$在[$\frac{1}{3}$,1]上递减,
ymin=a+1,ymax=3a+$\frac{1}{3}$,又2ymin>ymax.
则a<$\frac{5}{3}$,即有1≤a<$\frac{5}{3}$.
综上可得,存在这样的三角形,a的取值范围是$\frac{1}{15}$<a<$\frac{5}{3}$.
点评 本题考查不等式恒成立问题和存在性问题的解法,注意运用转化思想,转化为求最值,以及运用分类讨论的思想方法,注意对称轴或顶点与区间的关系,考查化简整理的运算能力,属于难题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | [0,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,$\frac{9}{4}$) | C. | [$\frac{1}{2}$,$\frac{9}{4}$] | D. | [$\frac{9}{4}$,+∞) |
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |
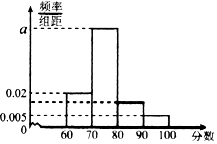 某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了m名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:
某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了m名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [60,70) | 16 | 0.2 |
| [70,80) | 50 | n |
| [80,90) | 10 | P |
| [90,100] | 4 | 0.05 |
| 合计 | M | I |
(II)如果用分层抽样的方法,从样本成绩在[60,70]和[90,100]的学生中共抽取5人,再从5人中选2人,求这2人成绩在[60,70]的概率.