��Ŀ����
2����֪��Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$����������Ϊ${F_1}��{F_2}��|{{F_1}{F_2}}|=2\sqrt{2}$����A��B����Բ�ϣ�F1���߶�AB�ϣ��ҡ�ABF2���ܳ�����$4\sqrt{3}$����1������ԲC�ı����̣�
��2����ԲO��x2+y2=4������һ��P����ԲC����������PM��PN��ԲO���ڵ�M��N�����PMN��������ֵ��
���� ��1������֪���a��c��ֵ�����������������b������Բ���̿���
��2����P��xP��yP������${{x}_{P}}^{2}+{{y}_{P}}^{2}=4$����������������һ�����ߵ�б�ʲ����ڣ����P�����ֱ꣬����á�PMN��������������ߵ�б�ʾ����ڣ���${x}_{P}�١�\sqrt{3}$��
�����P����Բ�����߷���Ϊy-yP=k��x-xP����������Բ���̣���Ϊ����x��һԪ���η��̣������б�ʽ����0�õ�����k�ķ��̣����ɸ���ϵ���Ĺ�ϵ�ɵ�PM��PN�����|MN|��д����������������û�������ʽ���������ֵ��
��� �⣺��1���ɡ�ABF2���ܳ�����$4\sqrt{3}$���ɵ�4a=4$\sqrt{3}$��a=$\sqrt{3}$��
��$|{F}_{1}{F}_{2}|=2\sqrt{2}$����c=$\sqrt{2}$����b2=a2-c2=1��
����Բ�ı�����Ϊ��$\frac{{x}^{2}}{3}+{y}^{2}=1$��
��2����P��xP��yP������${{x}_{P}}^{2}+{{y}_{P}}^{2}=4$��
����������������һ�����ߵ�б�ʲ����ڣ���${x}_{P}=��\sqrt{3}$��yP=��1��
��һ�����ߵ�б��Ϊ0���Ӷ�PM��PN����ʱ${S}_{��PMN}=\frac{1}{2}|PM|•|PN|=\frac{1}{2}��2��2\sqrt{3}=2\sqrt{3}$��
�����������ߵ�б�ʾ����ڣ���${x}_{P}�١�\sqrt{3}$��
�����P����Բ�����߷���Ϊy-yP=k��x-xP����������Բ���̣���ȥy�������ã�
��1+3k2��x2+6k��yP-kxP��x$+3��{y}_{P}-k{x}_{P}��^{2}-3=0$��
������á�=0����$��3-{{x}_{P}}^{2}��{k}^{2}+2{x}_{P}{y}_{P}k+1-{{y}_{p}}^{2}=0$��
������PM��PN��б�ʷֱ�Ϊk1��k2���Ӷ�${k}_{1}{k}_{2}=\frac{1-{{y}_{P}}^{2}}{3-{{x}_{P}}^{2}}=\frac{{{x}_{P}}^{2}-3}{3-{{x}_{P}}^{2}}=-1$��
��PM��PN�����߶�MNΪԲO��ֱ����|MN|=4��
��${S}_{��PMN}=\frac{1}{2}|PM|•|PN|��\frac{1}{4}��|PM{|}^{2}+|PN{|}^{2}��$=$\frac{1}{4}|MN{|}^{2}=4$��
���ҽ���|PM|=|PN|=2$\sqrt{2}$ʱ����PMNȡ���ֵ4��
���ϣ���PMN��������ֵΪ4��
���� ���⿼����Բ�ļ����ʣ�������ֱ������Բλ�ù�ϵ��Ӧ�ã�ѵ�������û�������ʽ����ֵ�����е��⣮

 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�| A�� | $\frac{f��e��}{e^2}��\frac{{f��{e^2}��}}{e}$ | B�� | $\frac{f��2��}{9}��\frac{f��3��}{4}$ | C�� | $\frac{f��2��}{e^2}��\frac{f��e��}{4}$ | D�� | $\frac{f��e��}{e^2}��\frac{f��3��}{9}$ |
| A�� | |a7|��|a8| | B�� | |a7|��|a8| | C�� | |a7|=|a8| | D�� | |a7|=0 |
| �ٷ��� | 85�ּ����� | 70�ֵ�84�� | 60�ֵ�69�� | 60������ |
| �ȼ� | A | B | C | D |
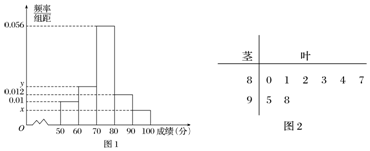
��1����n��Ƶ�ʷֲ�ֱ��ͼ��x��y��ֵ��
��2�������������������˼�룬���¼�������Ƶ����Ϊ��Ӧ�¼������ĸ��ʣ����ڸ�У��һѧ������ѡ3�ˣ���������1�˳ɼ��Ǻϸ�ȼ��ĸ��ʣ�
| A�� | $\frac{{\sqrt{2}}}{2}$ | B�� | $\sqrt{2}$ | C�� | $2\sqrt{2}$ | D�� | $\frac{{3\sqrt{2}}}{2}$ |