题目内容
已知集合A={x|
＜0}，B={x|1＜log2x＜2}，则A∩B=（ ）
| x-1 |
| x-3 |
| A、{x|0＜x＜3} |
| B、{x|2＜x＜3} |
| C、{x|1＜x＜3} |
| D、{x|1＜x＜4} |
考点：对数函数的单调性与特殊点
专题：不等式的解法及应用
分析：解分式不等式求得A，求对数不等式求得B，再根据两个集合的交集的定义求得A∩B．
解答：
解：由于集合A={x|
＜0}={x|（x-1）（x-3）＜0}={x|1＜x＜3}，B={x|1＜log2x＜2}={x|2＜x＜4}，
∴A∩B={x|2＜x＜3}，
故选：B．
| x-1 |
| x-3 |
∴A∩B={x|2＜x＜3}，
故选：B．
点评：本题主要考查分式不等式、对数不等式的解法，体现了等价转化的数学思想，属于基础题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
设袋中有8个红球，2个白球，若从袋中任取4个球，则其中恰有3个红球的概率为（ ）
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
若等比数列{an}满足a1a5=a3，则a3=（ ）
| A、1 | B、-1 |
| C、0或1 | D、-1或1 |
命题：“能被4整除的数一定是偶数”，其等价命题（ ）
| A、偶数一定能被4整除 |
| B、不是偶数不一定能被4整除 |
| C、不能被4整除的数不一定是偶数 |
| D、不是偶数一定不能被4整除 |
（文做）已知全集U={1，2，3，4，5，6，7}，集合A={1，3，4，6}则∁UA=（ ）
| A、{1，3，5，6} |
| B、{2，3，7} |
| C、{2，4，7} |
| D、{2，5，7} |
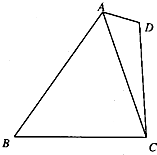如图所示，在四边形ABCD中，∠D=2∠B，且AD=1，CD=3，cosB=已知集合A={0，1}，B={x∈R|0＜x＜2}，则A∩B=（ ）
| A、{0} | B、{1} |
| C、[0，1] | D、（0，1） |