题目内容
1.点(a,b)在圆x2+y2=1内部,则直线ax+by-2=0与x2+y2=4的位置关系是相离.分析 由点(a,b)在圆x2+y2=1内部可得a2+b2<1,进而可得原点(0,0)到直线ax+by-2=0的距离d=$\frac{2}{\sqrt{{a}^{2}+{b}^{2}}}$>2,可判直线和圆的位置关系.
解答 解:∵点(a,b)在圆x2+y2=1内部,∴a2+b2<1,
∴原点(0,0)到直线ax+by-2=0的距离d=$\frac{2}{\sqrt{{a}^{2}+{b}^{2}}}$>2,
∴直线ax+by-2=0与x2+y2=4的位置关系是相离
故答案为:相离
点评 本题考查直线和圆的位置关系,涉及点到直线的距离公式,属基础题.

练习册系列答案
相关题目
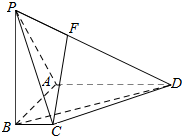 如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.
如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.