题目内容
12.已知函数f(x)是定义在R上的偶函数,且当x≥0时,f(x)=a|x-2|-a,其中a>0为常数,若函数y=f[f(x)]有10个零点,则a的取值范围是(1,3).分析 根据条件作出函数f(x)的图象,利用换元法转化为t=f(x)的方程根的个数问题,利用数形结合进行求解即可.
解答 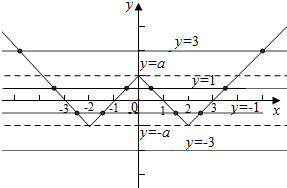 解:由已知可得:当a>0时,f(x)=a|x-2|-a=a(|x-2|-1)的图象如下图所示:
解:由已知可得:当a>0时,f(x)=a|x-2|-a=a(|x-2|-1)的图象如下图所示:
若f(x)=0,则(|x-2|-1=0,即|x-2|=1,则x=1或x=3,
∵函数f(x)是偶函数,∴x=-1,或x=-3也是函数的零点,
即函数f(x)的零点为x=±1,或x=±3,
设t=f(x),
则当t>a时,方程f(x)=t有2个交点,
当t=a时,方程f(x)=t有3个交点,
当-a<t<a时,方程f(x)=t有4个交点,
当t=-a时,方程f(x)=t有2个交点,
当t<-a时,方程f(x)=t有0个交点,
由y=f[f(x)]=0,得f(t)=0,
则t=±1,或t=±3,
若y=f[f(x)]有10个零点,则等价为f(x)=t分别有4,4,2,0个交点,
由对称性可知当t=1或t=-1时,各有4个交点,当t=3时有2个交点,当t=-3有0个交点,
即1<a<3,
故实数a的取值范围为:(1,3),
故答案为:(1,3)
点评 本题考查的知识点是函数的奇偶性,函数的零点,分类讨论思想,数形结合思想,综合性强,分类复杂,属于难题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
2.“女大学生就业难”究竟有多难?其难在何处?女生在求职中是否收到了不公平对待?通过对某大学应届毕业生的调查与实证分析试对下列问题提出解答.为调查某地区大学应届毕业生的调查,用简单随机抽样方法从该地区抽取了500为大学生做问卷调查,结果如下:
(1)估计该地区大学生中,求职中收到了公平对待的学生的概率;
(2)能否有99%的把握认为该地区的大学生求职中受到了不公平对待与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的大学生中,求职中是否受到了不公平对待学生的比例?说明理由.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 性别 是否公平 | 男 | 女 |
| 公平 | 40 | 30 |
| 不公平 | 160 | 270 |
(2)能否有99%的把握认为该地区的大学生求职中受到了不公平对待与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的大学生中,求职中是否受到了不公平对待学生的比例?说明理由.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.000 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
 如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面BB1C1C,AC⊥CC1.
如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面BB1C1C,AC⊥CC1.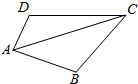 如图所示,已知四边形ABCD各边的长分别为AB=5,BC=5,CD=8,DA=3,且点A、B、C、D在同一个圆上,则对角线AC的长为$\frac{55}{7}$.
如图所示,已知四边形ABCD各边的长分别为AB=5,BC=5,CD=8,DA=3,且点A、B、C、D在同一个圆上,则对角线AC的长为$\frac{55}{7}$.