题目内容
若公比为q(q<0)的等比数列{an}的首项a1=-
,且满足an=
(n≥3)
(Ⅰ)求公比q的值;
(Ⅱ)设bn=log2an+12,求数列{
}的前n项和Sn.
| 1 |
| 2 |
| an-1+an-2 |
| 2 |
(Ⅰ)求公比q的值;
(Ⅱ)设bn=log2an+12,求数列{
| bn |
| 2n+1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)an=
(n≥3)∴an-2•q2=
即2q2-q-1=0解得即可;
(Ⅱ)∴bn=log2
=log2(
)n+1=-2(n+1),利用错位相减法求和即可.
| an-1+an-2 |
| 2 |
| an-2(q+1) |
| 2 |
(Ⅱ)∴bn=log2
| a | 2 n+1 |
| 1 |
| 4 |
解答:
解:(Ⅰ)∵an=
(n≥3)∴an-2•q2=
…(2分)
即2q2-q-1=0解得q=-
或q=1,
∵q<0,∴q=-
…(5分)
(Ⅱ)∵a1=-
∴an=(-
)n,
∴bn=log2
=log2(
)n+1=-2(n+1)…(7分)
则
=
…(8分)
Sn=-[
+
+
+…+
]
∴
Sn=-[
+
+
+…+
]
∴
Sn=-[1+
+
+…+
-
]=-[1+
-
]=-(
-
),…(11分)
∴Sn=-3+
…(12分)
| an-1+an-2 |
| 2 |
| an-2(q+1) |
| 2 |
即2q2-q-1=0解得q=-
| 1 |
| 2 |
∵q<0,∴q=-
| 1 |
| 2 |
(Ⅱ)∵a1=-
| 1 |
| 2 |
| 1 |
| 2 |
∴bn=log2
| a | 2 n+1 |
| 1 |
| 4 |
则
| bn |
| 2n+1 |
| -(n+1) |
| 2n |
Sn=-[
| 2 |
| 21 |
| 3 |
| 22 |
| 4 |
| 23 |
| n+1 |
| 2n |
∴
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| 4 |
| 24 |
| n+1 |
| 2n+1 |
∴
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| n+1 |
| 2n+1 |
| ||||
1-
|
| n+1 |
| 2n+1 |
| 3 |
| 2 |
| n+3 |
| 2n+1 |
∴Sn=-3+
| n+3 |
| 2n |
点评:本题主要考查等比数列的定义及性质,考查学生利用错位相减法对数列求和的能力及运算求解能力,属中档题.

练习册系列答案
相关题目
已知A、B、C为△ABC的三个内角,且关于x的方程(1+x2)sinA+2xsinB+(1-x2)sinC=0有两个相等实根,则△ABC的形状为( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等边三角形 |
某次数学测验中,学号为i(i=1,2,3,4)的四位同学的成绩f(i)∈{105,110,115,120}且满足f(1)≤f(2)≤f(3)≤f(4),则这四位同学的考试成绩的所有可能情况的种数为( )
| A、15 | B、25′ | C、35 | D、65 |
过原点和直线l1:x-3y+4=0与l2:2x+y+5=0的交点的直线的方程为( )
| A、19x-9y=0 |
| B、9x+19y=0 |
| C、3x+19y=0 |
| D、19x+3y=0 |
已知定义域为R的函数f(x)满足f(-x)=-f(x+4).当x>2时,f(x)单调递增.如果(x1-2)(x2-2)<0,f(x1)+f(x2)<0,则( )
| A、x1+x2=4 |
| B、x1+x2<4 |
| C、x1+x2>4 |
| D、x1+x2的值与4的大小无确定 |
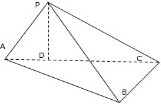 如图,在三棱锥P-ABC中,PD⊥面ABC于点D,且点D在AC上,PA=PB=PC=3,设AB=BC=
如图,在三棱锥P-ABC中,PD⊥面ABC于点D,且点D在AC上,PA=PB=PC=3,设AB=BC=