题目内容
5．直线$l：\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.$（t为参数）与圆C：（x+6）2+y2=25交于A，B两点，且$|{AB}|=\sqrt{10}$，则直线l的斜率为±$\frac{\sqrt{15}}{3}$．分析 直线$l：\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.$（t为参数）与圆C：（x+6）2+y2=25联立，可得t2+12tcosα+11=0，|AB|=|t1-t2|=$\sqrt{10}$⇒（t1+t2）2-4t1t2=10，即可得出结论．
解答 解：直线$l：\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.$（t为参数）与圆C：（x+6）2+y2=25联立，可得t2+12tcosα+11=0．
t1+t2=-12cosα，t1t2=11．
∴|AB|=|t1-t2|=$\sqrt{10}$⇒（t1+t2）2-4t1t2=10，⇒cos2α=$\frac{3}{8}$，tanα=±$\frac{\sqrt{15}}{3}$，
∴直线AB的斜率为±$\frac{\sqrt{15}}{3}$．
故答案为±$\frac{\sqrt{15}}{3}$．
点评 本题考查了直线参数方程及其应用，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
15．在边长为a的等边三角形ABC中，AD⊥BC于D，沿AD折成二面角B-AD-C后，BC=$\frac{1}{2}$a，这时二面角B-AD-C的大小为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{2}$ |
16．设z=1+i（i是虚数单位），O为坐标原点，若复数$\frac{2}{z}+{z^2}$在复平面内对应的向量为$\overrightarrow{OZ}$，则向量$\overrightarrow{OZ}$的模是（ ）
| A． | 1 | B． | 2 | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
20．
执行如图所示的程序框图，则输出的结果是（ ）
执行如图所示的程序框图，则输出的结果是（ ）| A． | 98 | B． | 99 | C． | 100 | D． | 101 |
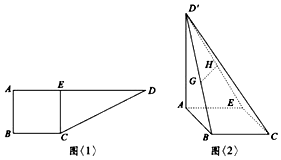如图＜1＞：在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC=2，AD=6，CE⊥AD于E点，把△DEC沿CE折到D'EC的位置，使$D'A=2\sqrt{3}$，如图＜2＞：若G，H分别为D'B，D'E的中点．