题目内容

2．已知曲线$f（x）=\frac{a}{x}（x＞0，a＞0）$上任一点P（x0，f（x0）），在点P处的切线与x，y轴分别交于A，B两点，若△OAB的面积为4，则实数a的值为（　　）
A．1B．2C．4D．8

分析 利用导数法确定切线方程y-$\frac{a}{{x}_{0}}$=-$\frac{a}{{{x}_{0}}^{2}}$（x-x0），从而解出点A，B的坐标，利用面积建立方程求出a的值．

解答 解：∵$f（x）=\frac{a}{x}（x＞0，a＞0）$，∴f′（x）=-$\frac{a}{{x}^{2}}$，
故f′（x0）=-$\frac{a}{{{x}_{0}}^{2}}$，
故直线l的方程为y-$\frac{a}{{x}_{0}}$=-$\frac{a}{{{x}_{0}}^{2}}$（x-x0），
令x=0得，y=$\frac{2a}{{x}_{0}}$，
令y=0得，x=2x0，
故S=$\frac{1}{2}$•$\frac{2a}{{x}_{0}}$•2x0=4，∴a=2
故选B．

点评 本题考查了导数的几何意义与导数的计算，属于中档题．

练习册系列答案
相关题目
12．运行如图所示的程序框图，则输出结果为（　　）
A．$\frac{11}{8}$B．$\frac{5}{4}$C．$\frac{3}{2}$D．$\frac{23}{16}$
13．已知集合A={a1，a2，…，an}，ai∈R，i=1，2，…，n，并且n≥2． 定义$T（A）=\sum_{1≤i＜j≤n}{|{a_j}-{a_i}}|$（例如：$\sum_{1≤i＜j≤3}{|{a_j}-{a_i}|}=|{a_2}-{a_1}|+|{a_3}-{a_1}|+|{a_3}-{a_2}|$）．
（Ⅰ）若A={1，2，3，4，5，6，7，8，9，10}，M={1，2，3，4，5}，集合A的子集N满足：N≠M，且T（M）=T（N），求出一个符合条件的N；
（Ⅱ）对于任意给定的常数C以及给定的集合A={a1，a2，…，an}，求证：存在集合B={b1，b2，…，bn}，使得T（B）=T（A），且$\sum_{i=1}^n{b_i}=C$．
（Ⅲ）已知集合A={a1，a2，…，a2m}满足：ai＜ai+1，i=1，2，…，2m-1，m≥2，a1=a，a2m=b，其中a，b∈R为给定的常数，求T（A）的取值范围．
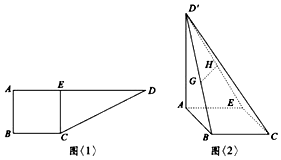10．如图＜1＞：在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC=2，AD=6，CE⊥AD于E点，把△DEC沿CE折到D'EC的位置，使$D'A=2\sqrt{3}$，如图＜2＞：若G，H分别为D'B，D'E的中点．
（Ⅰ）求证：GH⊥AD'；
（Ⅱ）求三棱锥D'-BCE的体积．
17．已知椭圆C1的中心在坐标原点，两焦点分别为双曲线${C_2}：\frac{x^2}{2}-{y^2}=1$的顶点，直线$x+\sqrt{2}y=0$与椭圆C1交于A，B两点，且点A的坐标为$（-\sqrt{2}，1）$，点P是椭圆C1上的任意一点，点Q满足$\overrightarrow{AQ}•\overrightarrow{AP}=0$，$\overrightarrow{BQ}•\overrightarrow{BP}=0$．
（1）求椭圆C1的方程；
（2）求点Q的轨迹方程；
（3）当A，B，Q三点不共线时，求△ABQ面积的最大值．
7．设x，y满足约束条件$\left\{\begin{array}{l}2x+y≤4\\ x-y≥-1\\ x-2y≤2\end{array}\right.$，则$z=\frac{x}{2}+y$的取值范围是$[-5，\frac{5}{2}]$．
14．已知两点$A（-\sqrt{2}，0），B（\sqrt{2}，0）$，动点P在y轴上的投影是Q，且$2\overrightarrow{PA}•\overrightarrow{PB}=|\overrightarrow{PQ}{|^2}$．
（Ⅰ）求动点P的轨迹C的方程；
（Ⅱ）过F（1，0）作互相垂直的两条直线交轨迹C于点G，H，M，N，且E1，E2分别是GH，MN的中点．求证：直线E1E2恒过定点．
11．（3a+2b）6的展开式中的第3项的二项式系数为15．（用数字作答）
12．已知在平面直角坐标系中，曲线C1的参数方程是$\left\{\begin{array}{l}x=-1+cosθ\\ y=sinθ\end{array}\right.$（θ为参数），以坐标原点为极点，x轴的正半轴为极轴，建立极坐标系，曲线C2的极坐标方程是ρ=2sinθ．
（Ⅰ） 求曲线C1与C2交点的平面直角坐标；
（Ⅱ） 点A，B分别在曲线C1，C2上，当|AB|最大时，求△OAB的面积（O为坐标原点）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网