如图是某几何体的三视图.其正视图.侧视图均为直径为2的半圆.俯视图是直径为2的圆.则该几何体的表面积为( )A．3πB．4πC．5πD．12π 题目和参考答案——青夏教育精英家教网—

题目内容

20．

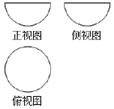如图是某几何体的三视图，其正视图，侧视图均为直径为2的半圆，俯视图是直径为2的圆，则该几何体的表面积为（　　）

A．

3π

B．

4π

C．

5π

D．

12π

分析由三视图可知：该几何体是一个直径为2的半球．即可得出．

解答解：由三视图可知：该几何体是一个直径为2的半球．
∴该几何体的表面积=$\frac{1}{2}×4π×{1}^{2}+π×{1}^{2}$=3π．
故选：A．

点评本题考查了球的三视图、表面积计算公式，考查了推理能力与计算能力，属于基础题．

练习册系列答案

中华活页文选初中文言文精讲精练系列答案

相关题目

6．

如图，四棱锥P-ABCD中，BC∥AD，BC=1，AD=2，AC⊥CD，且平面PCD⊥平面ABCD．
（1）求证：AC⊥PD；
（2）在线段PA上是否存在点E，使BE∥平面PCD？若存在，确定点E的位置，若不存在，请说明理由．

11．设m∈R，复数z₁=$\frac{{m}^{2}+m}{m+2}$+（m-15）i，z₂=-2+m（m-3）i，若z₁+z₂是虚数，求m的取值范围．

8．已知正实数x，y满足2x+y=2，则$\frac{2}{x}$+$\frac{1}{y}$的最小值为$\frac{9}{2}$．

15．在极坐标系中，求直线$θ=\frac{π}{4}（ρ∈R）$被曲线ρ=4sinθ所截得的弦长．

5．已知数列{a_n}为等差数列，其中a₂+a₃=8，a₅=3a₂．
（1）求数列{a_n}的通项公式；
（2）记${b_n}=\frac{2}{{{a_n}{a_{n+1}}}}$，设{b_n}的前n项和为S_n．求最小的正整数n，使得${S_n}＞\frac{2016}{2017}$．

12．已知函数f（x）=$\left\{\begin{array}{l}{sin\frac{πx}{6}，0≤x≤2}\\{2f（x-2），x＞2}\end{array}\right.$，则f（2017）等于（　　）

2¹⁰⁰⁷

2¹⁰⁰⁸

9．若x，y满足约束条件$\left\{\begin{array}{l}x-y+1≤0\\ x-2y≤0\\ x+2y-2≤0\end{array}\right.$，则z=x+y的最大值为（　　）

10．已知$P：{x^2}-2x＜0，Q：\frac{x+3}{x-1}≤0$，若P真Q假，则x的取值范围是（　　）

试题分类