题目内容
若实数a，b满足ab=1，求a+b的取值范围．
考点：基本不等式
专题：不等式的解法及应用
分析：由ab=1，变形为b=
．可得a+b=a+
．通过对a分类讨论，利用基本不等式的性质即可得出．
| 1 |
| a |
| 1 |
| a |
解答：
解：∵ab=1，∴b=
．
∴a+b=a+
．
当a＞0时，a+
≥2
=2，当且仅当a=1时取等号．
同理当a＜0时，a+
≤-2，当且仅当a=-1时取等号．
综上可得：a+b的取值范围是（-∞，-2]∪[2，+∞）．
| 1 |
| a |
∴a+b=a+
| 1 |
| a |
当a＞0时，a+
| 1 |
| a |
a•
|
同理当a＜0时，a+
| 1 |
| a |
综上可得：a+b的取值范围是（-∞，-2]∪[2，+∞）．
点评：本题考查了基本不等式的性质、分类讨论的思想方法，属于基础题．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
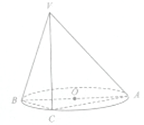如图，AB是⊙0的直径，点C是⊙0上的点，过点C的直线VC垂直于⊙0所在平面，且AC=