题目内容
已知函数f(x)=
(1)若函数f(x)在(-∞,1]上为减函数,则实数a的取值范围是 ;
(2)若函数f(x)在R上为减函数,则实数a的取值范围是 .
|
(1)若函数f(x)在(-∞,1]上为减函数,则实数a的取值范围是
(2)若函数f(x)在R上为减函数,则实数a的取值范围是
考点:分段函数的应用,函数单调性的性质
专题:计算题,函数的性质及应用
分析:(1)由一次函数的单调性,即可得到;
(2)由于函数f(x)在R上为减函数,则0<a<1,且2-3a<0,还必须a≤2-3a+1,解出它们,再求并即可.
(2)由于函数f(x)在R上为减函数,则0<a<1,且2-3a<0,还必须a≤2-3a+1,解出它们,再求并即可.
解答:
解:(1)当x≤1时,f(x)=(2-3a)x+1,
∵函数f(x)在(-∞,1]上为减函数,∴2-3a<0,
即a>
;
(2)∵函数f(x)在R上为减函数,
∴
即
,
∴
<a≤
.
故答案为:(
,+∞),(
,
].
∵函数f(x)在(-∞,1]上为减函数,∴2-3a<0,
即a>
| 2 |
| 3 |
(2)∵函数f(x)在R上为减函数,
∴
|
|
∴
| 2 |
| 3 |
| 3 |
| 4 |
故答案为:(
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
点评:本题考查函数的性质和应用,主要考查函数的单调性及运用,注意函数的定义域,是一道易错题.

练习册系列答案
相关题目
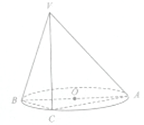 如图,AB是⊙0的直径,点C是⊙0上的点,过点C的直线VC垂直于⊙0所在平面,且AC=
如图,AB是⊙0的直径,点C是⊙0上的点,过点C的直线VC垂直于⊙0所在平面,且AC=