题目内容
已知函数 .
.
(1)求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)设 ,如果过点
,如果过点 可作曲线
可作曲线 的三条切线,证明:
的三条切线,证明: .
.
(1) (2)根据已知函数求解导数,进一步分析方程有三个实数根来分析得到证明。
(2)根据已知函数求解导数,进一步分析方程有三个实数根来分析得到证明。
解析试题分析:解:(1)求函数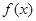 的导数;
的导数; .
.
曲线 在点
在点 处的切线方程为:
处的切线方程为: ,即
,即 .
.
(2)如果有一条切线过点 ,则存在
,则存在 ,使
,使 .
.
于是,若过点 可作曲线
可作曲线 的三条切线,则方程
的三条切线,则方程
有三个相异的实数根.记  ,则
,则 
 .
.
当 变化时,
变化时, 变化情况如下表:
变化情况如下表:

0 




0 
0 


极大值 

极小值 

综上,如果过 可作曲线
可作曲线 三条切线,即
三条切线,即 有三个相异的实数根,则
有三个相异的实数根,则
即  .
.
考点:导数在研究函数中的运用
点评:解决该试题的关键是对于导数的几何意义的运用,以及能结合方程根问题求解a,b的不等关系式。属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在区间
在区间 上最大值是5,最小值是-11,求
上最大值是5,最小值是-11,求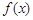 的解析式.
的解析式.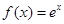 ,其图像在点
,其图像在点 处的切线为
处的切线为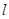 .
. 、直线
、直线 及两坐标轴围成的图形绕
及两坐标轴围成的图形绕 轴旋转一周所得几何体的体积;
轴旋转一周所得几何体的体积; 轴围成图形的面积.
轴围成图形的面积. 在
在 处取得极值,并且它的图象与直线
处取得极值,并且它的图象与直线 在点( 1 , 0 ) 处相切, 求a , b , c的值.
在点( 1 , 0 ) 处相切, 求a , b , c的值. ,设曲线y=
,设曲线y= 在与x轴交点处的切线为y=4x-12,
在与x轴交点处的切线为y=4x-12,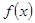 为
为
 ,求函数g(x)在[0,m]上的最大值。
,求函数g(x)在[0,m]上的最大值。 ,若对一切
,若对一切 ,不等式
,不等式 恒成立,求实数t的取值范围
恒成立,求实数t的取值范围 (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切. )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围; 成立;
成立; .
. .
. ,
, 在
在 恒成立(其中
恒成立(其中 表示
表示 的导函数),求
的导函数),求 的最大值;
的最大值; 在
在 上有且仅有一个实根,求
上有且仅有一个实根,求 的取值范围.
的取值范围. .
. 在区间
在区间 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论; 时,
时, 恒成立,求整数
恒成立,求整数 的最大值;
的最大值; .
.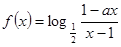 为奇函数,a为常数。
为奇函数,a为常数。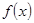 在区间
在区间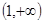 上为增函数;
上为增函数; 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m 的取值范围。
恒成立,求实数m 的取值范围。