题目内容
17.若函数f(x)=(x+1)2-alnx在区间(0,+∞)内任取有两个不相等的实数x1,x2,不等式$\frac{{f({{x_1}+1})-f({{x_2}+1})}}{{{x_1}-{x_2}}}$>1恒成立,则a的取值范围是( )| A. | (-∞,3) | B. | (-∞,-3) | C. | (-∞,3] | D. | (-∞,-3] |
分析 由条件可知f′(x)>1在(1,+∞)上恒成立,分离参数得a<2x(x+1)-1,求出函数的最小值即可得出a的范围.
解答 解:∵$\frac{{f({{x_1}+1})-f({{x_2}+1})}}{{{x_1}-{x_2}}}$>1恒成立,
∴f′(x)=2(x+1)-$\frac{a}{x}$>1在(1,+∞)上恒成立,
∴a<2x(x+1)-x=2x2+x在(1,+∞)恒成立,
令g(x)=2x2+x,则g(x)的图象开口向上,对称轴为x=-$\frac{1}{4}$,
∴g(x)>g(1)=3,
∴a≤3.
故选C.
点评 本题考查了函数的恒成立问题研究,函数最值得计算,属于中档题.

练习册系列答案
相关题目
7.某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
(1)从编号1-5的五位推销员中随机取出两位,求他们年推销金额之和不少于7万元的概率;
(2)求年推销金额y关于工作年限x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;若第6名产品推销员的工作年限为11年,试估计他的年推销金额.
附:回归直线的斜率和截距的最小二乘法估计公式为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{(x}_{i}-\overline{x}){(x}_{i}-\overline{y})}{{\sum_{i=1}^{n}{(x}_{i}-\overline{x})}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x年 | 3 | 5 | 6 | 7 | 9 |
| 年推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
(2)求年推销金额y关于工作年限x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;若第6名产品推销员的工作年限为11年,试估计他的年推销金额.
附:回归直线的斜率和截距的最小二乘法估计公式为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{(x}_{i}-\overline{x}){(x}_{i}-\overline{y})}{{\sum_{i=1}^{n}{(x}_{i}-\overline{x})}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
5.在区间[-1,0]上任取两实数x、y,则y<3x的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
2.(1-x)5(1+$\sqrt{x}$)2的展开式中x4的系数为( )
| A. | -10 | B. | -5 | C. | 10 | D. | 15 |
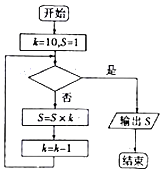 执行如图所示的储蓄框图,若输出S的值为720,则判断框内可填入的条件是k≤7?.
执行如图所示的储蓄框图,若输出S的值为720,则判断框内可填入的条件是k≤7?.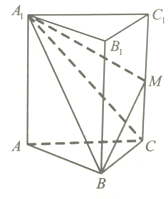 如图,在直三棱柱中ABC-A1B1C1中,二面角A-A1B-C是直二面角,AB=BC═2,点M是棱CC1的中点,三棱锥M-BCA1的体积为1.
如图,在直三棱柱中ABC-A1B1C1中,二面角A-A1B-C是直二面角,AB=BC═2,点M是棱CC1的中点,三棱锥M-BCA1的体积为1.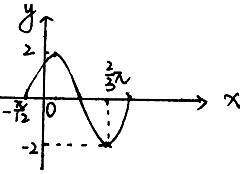 若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),如图所示
若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),如图所示