题目内容
已知
+y2=1，F1，F2分别为其左右焦点，P为椭圆上一点，则∠F1PF2的取值范围是 ．
| x2 |
| 4 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：当点P取短轴的一个端点A（0，1）时，∠F1PF2的取得最大值．再利用椭圆的标准方程、直角三角形的边角关系即可得出．
解答：
解：当点P取短轴的一个端点A（0，1）时，∠F1PF2的取得最大值．
∵tan∠F1AO=
=
，∴∠F1AO=
，
∴∠F1PF2=
．
∴∠F1PF2的取值范围是[0，
]．
故答案为：[0，
]
∵tan∠F1AO=
| c |
| b |
| 3 |
| π |
| 3 |
∴∠F1PF2=
| 2π |
| 3 |
∴∠F1PF2的取值范围是[0，
| 2π |
| 3 |
故答案为：[0，
| 2π |
| 3 |
点评：本题考查了椭圆的标准方程及其性质、直角三角形的边角关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
发散思维新课堂系列答案
相关题目
已知函数f（x）=log2x，且函数y=g（x）的图象与函数y=f（x）的图象关于直线y=x对称，则函数g（x2）是（ ）
| A、奇函数且在（0，+∞）上是减函数 |
| B、偶函数且在（0，+∞）上是增函数 |
| C、奇函数且在（-∞，0）上是减函数 |
| D、偶函数且在（-∞，0）上是增函数 |
原点到直线3x+2y-13=0的距离是（ ）
A、
| ||
| B、4 | ||
| C、1 | ||
D、
|
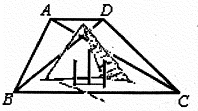如图，在一座底部不可到达的孤山两侧，有两段平行的公路AB和CD，现测得AB=5，AC=9∠BCA=30°，∠ADB=45°
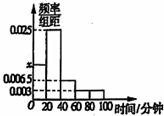某学校随机抽取部分新生调查其上学所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学所需时间的范围是[0，100]，样本数据分组为：[0，20），[20，40），[40，60）[60，820），[80，100]，则