题目内容
2.由曲线y=x3与直线y=4x所围成的平面图形的面积为( )| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
分析 根据题意,得到积分上限为2,积分下限为-2的积分,从而利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可.
解答  解:根据题意,得到积分上限为2,积分下限为-2,
解:根据题意,得到积分上限为2,积分下限为-2,
曲线y=x3与直线所围成的图形的面积是∫-22(4x-x3)dx,
而∫-22(4x-x3)dx=(2x2-$\frac{1}{4}$x4)|-22=8
∴曲边梯形的面积是8,
故选:B.
点评 本题考查学生利用定积分求曲边梯形的面积,会求出原函数的能力,同时考查了数形结合的思想,属于中档题.

练习册系列答案
相关题目
10.已知集合A={x∈R|x≤1},B={x∈R|x2≤4},A∩B=( )
| A. | (-∞,2] | B. | [-2,2] | C. | [1,2] | D. | [-2,1] |
7.已知tanθ=2,则$\frac{sinθ}{si{n}^{3}θ-co{s}^{3}θ}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{10}{7}$ | D. | $\frac{3}{2}$ |
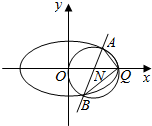 如图,已知焦点在x轴上的椭圆C过点(-2,0),且离心率为$\frac{\sqrt{3}}{2}$,Q为椭圆C的右顶点.
如图,已知焦点在x轴上的椭圆C过点(-2,0),且离心率为$\frac{\sqrt{3}}{2}$,Q为椭圆C的右顶点.