题目内容
已知函数f（x）=x3-3x，x∈[-a，a]，a＞0，若f（x）在[-a，a]上是减函数，求实数a的取值范围．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：由f′（x）≤0得函数的递减区间[-1，1]，由题意即可得出a的范围．
解答：
解：f′（x）=3x2-3=3（x+1）（x-1）≤0，
∴-1≤x≤1，
∵函数f（x）=x3-3x，在[-a，a]上是减函数，且a＞0，
∴0＜a≤1．
∴实数a的取值范围是（0，1]．
∴-1≤x≤1，
∵函数f（x）=x3-3x，在[-a，a]上是减函数，且a＞0，
∴0＜a≤1．
∴实数a的取值范围是（0，1]．
点评：本题考查利用导数判断函数的单调性，属于基础题．
练习册系列答案
相关题目
已知P（x，y）为区域
内的任意一点，当该区域的面积为4时，z=2x-y的
最大值是（ ）
|
最大值是（ ）
| A、6 | ||
| B、0 | ||
| C、2 | ||
D、2
|
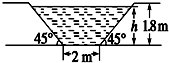如图，某灌溉渠的横断面是等腰梯形，底宽为2m，渠深为1.8m，斜坡的倾斜角是45°．（临界状态不考虑）