题目内容
13.(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求a≥b的概率;(2)甲、乙两人约定在6时到7时之间在某处会面,并约定先到者应等候另一人一刻种,过时即可离去.求两人能会面的概率.
分析 (1)确定所有基本事件个数,满足a≥b的事件数,然后直接利用古典概型概率计算公式求解;
(2)以x轴和y轴分别表示甲、乙两人到达约定地点的时间,若两人能够会面则|x-y|≤15.,由测度比是面积比求概率.
解答  解:(1)基本事件共有12个,其中a≥b基本事件包括(0,0),(1,1),(2,2),(1,0),(2,0),(2,1),(3,0),(3,1)(3,2)9个基本事件,所以a≥b的概率为:$\frac{9}{12}$=$\frac{3}{4}$;
解:(1)基本事件共有12个,其中a≥b基本事件包括(0,0),(1,1),(2,2),(1,0),(2,0),(2,1),(3,0),(3,1)(3,2)9个基本事件,所以a≥b的概率为:$\frac{9}{12}$=$\frac{3}{4}$;
(2)以x轴和y轴分别表示甲、乙两人到达约定地点的时间,若两人能够会面则|x-y|≤15.
在如图所示平面直角坐标系下,(x,y)的所有可能结果是边长为60的正方形区域,而事件A“两人能够会面”的可能结果由图中的阴影部分表示.由几何概型的概率公式得:P(A)=$\frac{6{0}^{2}-4{5}^{2}}{6{0}^{2}}$=$\frac{7}{16}$,所以,两人能会面的概率是$\frac{7}{16}$.
点评 本题考查了古典概型及其概率计算公式,考查了几何概型的概率,关键是理解(2)的测度比,是中档题.

练习册系列答案
相关题目
4.已知集合M={x|y=ln(x2-3x-4)},N={y|y=2x-1},则M∩N等于( )
| A. | {x|x>4} | B. | {x|x>0} | C. | {x|x<-1} | D. | {x|x>4或x<-1} |
5.cos6°cos36°+sin6°cos54°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 0 | D. | $-\frac{1}{2}$ |
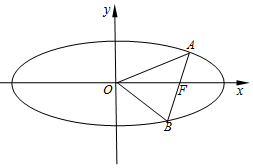 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,过右焦点F的直线l交椭圆于A、B两点,当l与x轴垂直时,AB长为$\frac{{4\sqrt{3}}}{3}$.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,过右焦点F的直线l交椭圆于A、B两点,当l与x轴垂直时,AB长为$\frac{{4\sqrt{3}}}{3}$.