题目内容
已知方程x2+（1+a）x+1+a+b=0的两根为x1，x2，并且0＜x1＜1＜x2，则
的取值范围是 ．
| b |
| a |
考点：一元二次方程的根的分布与系数的关系
专题：函数的性质及应用
分析：构建函数f（x）=x2+（2+a）x+1+a+b，利用方程x2+（2+a）x+1+a+b=0的两根为x1，x2，并且0＜x1＜1＜x2，确定满足条件的可行域，再利用数形结合即可得到结论．
解答：
解：构建函数f（x）=x2+（2+a）x+1+a+b
∵方程x2+（2+a）x+1+a+b=0的两根为x1，x2，
并且0＜x1＜1＜x2，
∴
，即
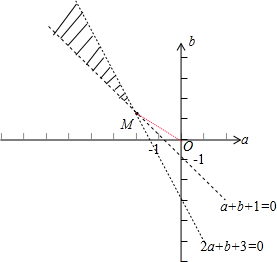
，不等式组对应的平面区域如下图阴影示：
两直线的交点坐标为M（-2，1），
∵
=
表示阴影区域上一点与原点连线的斜率，
由图可知
∈（-∞，-
），
故答案为：（-∞，-
）．
解：构建函数f（x）=x2+（2+a）x+1+a+b∵方程x2+（2+a）x+1+a+b=0的两根为x1，x2，
并且0＜x1＜1＜x2，
∴
|
|
两直线的交点坐标为M（-2，1），
∵
| b |
| a |
| b-0 |
| a-0 |
由图可知
| b |
| a |
| 1 |
| 2 |
故答案为：（-∞，-
| 1 |
| 2 |
点评：本题考查的知识点是一元二次方程的根的分布与系数的关系，三个二次之间的关系，线性规划，其中构建函数，利用线性规划知识求解是解答本题的关键，属于基础题．
练习册系列答案
相关题目
为了了解我校2012年高考准备报考“体育特长生”的学生体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为12，则报考“体育特长生”的学生人数是
如图，△BCD是等边三角形，AB=AD，∠BAD=90°，将△BCD沿BD折叠到△BCD的位置，使得AD⊥C′B．