题目内容
设点M是线段BC的中点，点A在直线BC外，
2=16，|
+
|=|
-
|，则|
|=（ ）
| BC |
| AB |
| AC |
| AB |
| AC |
| AM |
| A、2 | B、4 | C、6 | D、8 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由于|
+
|=|
-
|，点A在直线BC外，可得以AB，AC为邻边的平行四边形为矩形，利用矩形的对角线的性质即可得出．
| AB |
| AC |
| AB |
| AC |
解答：
解：∵|
+
|=|
-
|，点A在直线BC外，如图所示，
∴以AB，AC为邻边的平行四边形的对角线相等，因此四边形为矩形，
∴|AM|=
|BC|=
×4=2．
故选：A．
| AB |
| AC |
| AB |
| AC |
∴以AB，AC为邻边的平行四边形的对角线相等，因此四边形为矩形，
∴|AM|=
| 1 |
| 2 |
| 1 |
| 2 |
故选：A．
点评：本题考查了向量的平行四边形法则、矩形的对角线的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
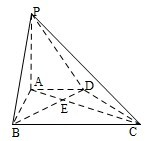四棱锥P-ABCD中，ABCD为直角梯形，AD∥BC，∠ABC=90°，PA⊥面ABCD，PA=3，AD=2，AB=2