题目内容
若f(x)=
,g(x)=x2-x(x∈R),则方程f[g(x)]=x的解为 .
|
考点:分段函数的应用
专题:函数的性质及应用
分析:根据分段函数的表达式,求出g(x)=2的解,然后代入解方程f[g(x)]=x即可得到结论.
解答:
解:由g(x)=x2-x=2得,x=-1或x=2,
即当x≥2或x≤-1时,g(x)≥2,
当-1<x<2时,g(x)<2,
①若x≥2或x≤-1时,g(x)≥2,
此时f[g(x)]=x等价为g(x)-1=x,即x2-x-1=x,整理得x2-2x-1=0,
解得x=1+
或x=1-
(舍掉).
②若-1<x<2时,g(x)<2,
此时f[g(x)]=x等价为1=x,即x=1,
综上方程的解为x=1或x=1+
,
故答案为:1或x=1+
即当x≥2或x≤-1时,g(x)≥2,
当-1<x<2时,g(x)<2,
①若x≥2或x≤-1时,g(x)≥2,
此时f[g(x)]=x等价为g(x)-1=x,即x2-x-1=x,整理得x2-2x-1=0,
解得x=1+
| 2 |
| 2 |
②若-1<x<2时,g(x)<2,
此时f[g(x)]=x等价为1=x,即x=1,
综上方程的解为x=1或x=1+
| 2 |
故答案为:1或x=1+
| 2 |
点评:本题主要考查分段函数的应用,利用分类讨论的思想是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
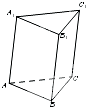 如图,在三棱柱ABC-A1B1C1中,侧棱AA1与侧面BCC1B1的距离为2,侧面BCC1B1的面积为4,此三棱柱ABC-A1B1C1的体积为
如图,在三棱柱ABC-A1B1C1中,侧棱AA1与侧面BCC1B1的距离为2,侧面BCC1B1的面积为4,此三棱柱ABC-A1B1C1的体积为 如图所示,△ABC是边长为3的正三角形,若在每一边的两个三等分点中,各随机选取一点连成三角形,下列命题正确的是(写出所有正确命题的编号):
如图所示,△ABC是边长为3的正三角形,若在每一边的两个三等分点中,各随机选取一点连成三角形,下列命题正确的是(写出所有正确命题的编号):