题目内容
13.若变量x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{x-y+2≥0}\\{x-2≤0}\end{array}\right.$,n=2x+y-2,则 取最大值时,(2$\sqrt{x}$+$\frac{1}{x}$)n二项展开式中的常数项为240.分析 首先利用约束条件得到可行域,结合n的几何意义求出其最大值,然后对二项式的通项求常数项.
解答 解:已知得到可行域如图:n=2x+y-2变形为y=-2x+2+z,当此直线经过图中B(2,4)时,直线在y轴的截距最大,z最大,所以z 的最大值为2×2+4-2=6,
所以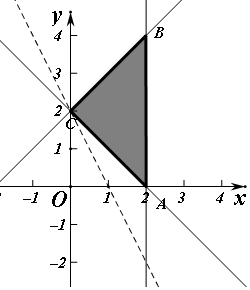 (2$\sqrt{x}$+$\frac{1}{x}$)n二项展开式中的通项为${C}_{6}^{r}(2\sqrt{x})^{r}(\frac{1}{x})^{6-r}={2}^{r}{C}_{6}^{r}{x}^{\frac{3}{2}r-6}$,
(2$\sqrt{x}$+$\frac{1}{x}$)n二项展开式中的通项为${C}_{6}^{r}(2\sqrt{x})^{r}(\frac{1}{x})^{6-r}={2}^{r}{C}_{6}^{r}{x}^{\frac{3}{2}r-6}$,
当r=4此项为常数项,所以常数项为24${C}_{6}^{4}$=240;
故答案为:240.
点评 本题考查了简单线性规划问题与二项式定理的运用;关键是利用数形结合正确求出n,然后由二项展开式通项求常数项.

练习册系列答案
相关题目
8.下列命题中正确的是( )
| A. | 若?服从正态分布N(1,2),且P(?>2)=0.1,则P(0<?<2)=0.2 | |
| B. | 命题:“?x>1,x2>1”的否定是“?x≤1,x2≤1” | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
5.已知数列{an}前n项和满足Sn-Sn-1=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$ (n≥2),a1=1,则an=( )
| A. | n | B. | 2n-1 | C. | n2 | D. | 2n2-1 |
2.已知函数f(x)=($\frac{1}{3}$)x,a>0,b>0,a≠b,m=f($\frac{a+b}{2}$),n=f($\sqrt{ab}$),p=f($\frac{2ab}{a+b}$),则m,n,p 的大小关系为( )
| A. | m<n<p | B. | m<p<n | C. | p<m<n | D. | p<n<m |
3.已知向量$\overrightarrow{a}$=(cosθ,sinθ),θ∈(0,π),$\overrightarrow{b}$=(1,$\sqrt{3}$),若$\overrightarrow{a}$与$\overrightarrow{b}$共线,则sin2θ=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |