题目内容
3．某地汽车站在6：00～6：10内任何时刻发出第1班车，在6：10～6：20任何时刻发出第2班车，某人在6：00～6：20的任何时刻到达车站是等可能的，求此人乘坐前2班车的概率．分析 根据题意，利用对立事件的概率，求出坐不到第1、第2班车的概率，再求能乘坐前2班车的概率．
解答 解：坐不到车的话只能在6：10～6：20，
概率为$\frac{20-10}{20-0}$=$\frac{1}{2}$；
在这段时间坐不到第2班车的概率为$\frac{1}{2}$；
故坐不到第1、第2班车的概率为$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$；
所以此人乘坐前2班车的概率为P=1-$\frac{1}{4}$=$\frac{3}{4}$．
点评 本题考查了概率的计算问题，是基础题目．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
相关题目
18．
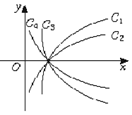图中曲线是对数函数y=logax的图象，已知a取$\sqrt{3}$，$\frac{4}{3}$，$\frac{3}{5}$，$\frac{1}{10}$四个值，则相应于C1，C2，C3，C4的a值依次为（ ）
图中曲线是对数函数y=logax的图象，已知a取$\sqrt{3}$，$\frac{4}{3}$，$\frac{3}{5}$，$\frac{1}{10}$四个值，则相应于C1，C2，C3，C4的a值依次为（ ）| A． | $\frac{4}{3}$，$\sqrt{3}$，$\frac{3}{5}$，$\frac{1}{10}$ | B． | $\sqrt{3}$，$\frac{4}{3}$，$\frac{1}{10}$，$\frac{3}{5}$ | C． | $\sqrt{3}$，$\frac{4}{3}$，$\frac{3}{5}$，$\frac{1}{10}$ | D． | $\frac{4}{3}$，$\sqrt{3}$，$\frac{1}{10}$，$\frac{3}{5}$ |
8．若命题“p且q”为假，且p为真，则（ ）
| A． | “p或q”为假 | B． | q为假 | C． | q为真 | D． | 不能判断q的真假 |
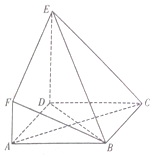如图，四边形ABCD是正方形，DE⊥平面ABCD，AF∥DE，AF=$\frac{1}{2}AD=\frac{1}{3}$ED=1．
12．已知3x+x3=100，[x]表示不超过x的最大整数，则[x]=（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |