题目内容
18.数列{an}满足a1=2,an+1+an=2n+3.(1)求a2,a3,a4;
(2)求an的表达式.
分析 (1)利用递推关系式逐步求解即可.
(2)方法一:猜想通项公式,利用数学归纳法证明即可.
方法二:利用递推关系式,逐步代换求解即可;
方法三:图象数列偶数项是等差数列,奇数项是等差数列,分别求解通项公式即可.
解答 解:(1)a1=2,an+1+an=2n+3,a2=3,a3=4,a4=5;
(2)方法一:猜想an的表达式为:${a_n}=n+1({n∈{N^*}})$,
下面用数学归纳法证明:①a1=2,猜想成立;
②假设n=k(k∈N*)时,ak=k+1,则ak+1=-ak+2k+3=-(k+1)+2k+3=(k+1)+1,即n=k+1时猜想成立,
综合①②,由数学归纳法原理知:${a_n}=n+1({n∈{N^*}})$…(12分)
方法二:由an+1+an=2n+3得:${a_{n+1}}-({n+2})=-[{{a_n}-({n+1})}]=…={({-1})^n}({{a_1}-2})=0$,
所以:${a_n}=n+1({n∈{N^*}})$…(12分)
方法三:由an+1+an=2n+3得:an+2+an+1=2n+5,两式作差得:an+2-an=2,
于是a1,a3,a5,…是首项a1=2,公差为2的等差数列,那么${a_{2k-1}}=2k({k∈{N^*}})$,
且a2,a4,a6,…是首项a2=3,公差为2的等差数列,那么${a_{2k}}=2k+1({k∈{N^*}})$,
综上可知:${a_n}=n+1({n∈{N^*}})$…(12分)
点评 本题考查数列的递推关系式的应用,数列的通项公式的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
8.若命题“p且q”为假,且p为真,则( )
| A. | “p或q”为假 | B. | q为假 | C. | q为真 | D. | 不能判断q的真假 |
9.设定义在R上的函数f(x)满足对任意x∈R都有f(x)+f(2-x)=2,若函数g(x)=$\frac{x}{x-1}$与f(x)图象的交点为(x1,y1),(x2,y2),…,(xn,yn),则$\sum_{i=1}^{n}$(xi+yi)=( )
| A. | n | B. | 2n | C. | 3n | D. | 4n |
10.函数f(x)=ax2+4(a+1)x-3在[2,+∞)上递减,则a的取值范围是( )
| A. | a≤-$\frac{1}{2}$ | B. | -$\frac{1}{2}$≤a<0 | C. | 0<a≤$\frac{1}{2}$ | D. | a≥$\frac{1}{2}$ |
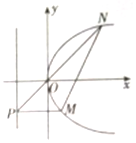 双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3}=1(a>0)$的左、右焦点分别为F1,F2,过F2作x轴垂直的直线交双曲线C于A、B两点,△F1AB的面积为12,抛物线E:y2=2px(p>0)以双曲线C的右顶点为焦点.
双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3}=1(a>0)$的左、右焦点分别为F1,F2,过F2作x轴垂直的直线交双曲线C于A、B两点,△F1AB的面积为12,抛物线E:y2=2px(p>0)以双曲线C的右顶点为焦点.