题目内容
已知两函数f(x)=x2+2x,g(x)=-x2+a,当a= 时,f(x),g(x)的图象有且只有一条公切线,该公切线的方程为 .
考点:二次函数的性质
专题:导数的概念及应用
分析:根据已知条件知f(x),g(x)的图象只有一个公共点,所以方程x2+2x=-x2+a只有一个解,这样便可求得a=-
,并求得公共点为(-
,-
).而该点便是切点,所以通过求f′(x)便能得到该切线的斜率,由点斜式方程即可写出公切线的方程.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
解答:
解:要使f(x)与g(x)的图象只有一条公切线,则需使f(x),g(x)图象有一个公共点;
∴由f(x)=g(x)得,x2+2x=-x2+a,整理成:
2x2+2x-a=0,①,该方程只有一个解;
∴△=4+8a=0,∴a=-
,带入方程①得2x2+2x+
=0;
解得,x=-
,f(-
)=-
;
∴切点为(-
,-
),f′(x)=2x+2,f′(-
)=1;
即切线的斜率为1;
∴切线方程为y+
=x+
;
即y=x-
.
故答案为:-
,y=x-
.
∴由f(x)=g(x)得,x2+2x=-x2+a,整理成:
2x2+2x-a=0,①,该方程只有一个解;
∴△=4+8a=0,∴a=-
| 1 |
| 2 |
| 1 |
| 2 |
解得,x=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
∴切点为(-
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
即切线的斜率为1;
∴切线方程为y+
| 3 |
| 4 |
| 1 |
| 2 |
即y=x-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
| 1 |
| 2 |
点评:考查曲线的公共点和曲线方程形成方程组解的关系,一元二次方程解的情况和判别式△的关系,函数在切点处的导数值与切线斜率的关系,以及直线的点斜式方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

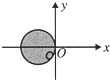

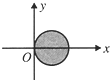
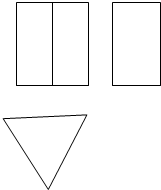 如图所示是一个几何体的三视图,若其正视图的面积为4cm2,俯视图的面积为
如图所示是一个几何体的三视图,若其正视图的面积为4cm2,俯视图的面积为