题目内容
1.已知圆C:(x-a)2+(y-2)2=4(a>0)与直线l:x-y+3=0交于两点A,B.(1)当直线l被圆C截得的弦长为$2\sqrt{2}$时,求a的值;
(2)若圆上存在点P,满足$\overrightarrow{CA}+\overrightarrow{CB}=\overrightarrow{CP}$,求a的值.
分析 (1)由题意,圆心到直线的距离d=$\frac{|a-2+3|}{\sqrt{2}}$=$\sqrt{4-2}$,即可求a的值;
(2)由题意,圆心到直线的距离d=$\frac{|a-2+3|}{\sqrt{2}}$=$\frac{1}{2}×2$,即可求a的值.
解答 解:(1)由题意,圆心到直线的距离d=$\frac{|a-2+3|}{\sqrt{2}}$=$\sqrt{4-2}$,∴a=1或-3;
(2)由题意,圆心到直线的距离d=$\frac{|a-2+3|}{\sqrt{2}}$=$\frac{1}{2}×2$,∴a=-1±$\sqrt{2}$.
点评 本题考查直线与圆的位置关系,考查弦长的计算,考查向量知识的运用,属于中档题.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
12.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
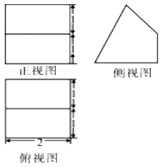

| A. | 3cm3 | B. | 5cm3 | C. | 4cm3 | D. | 6cm3 |
9.不等式3≤|5-2x|<9的解集为( )
| A. | [-2,1)∪[4,7) | B. | (-2,1]∪[4,7] | C. | (-2,1]∪(4,7) | D. | (-2,1]∪[4,7) |
16.一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )

| A. | 36 | B. | 48 | C. | 64 | D. | 72 |
6.执行如图所示的程序框图,若输入a的值为2,则输出b( )


| A. | -2 | B. | 1 | C. | 2 | D. | 4 |
10.已知数列{an},若点(n,an)(n∈N*)在经过点(10,6)的定直线l上,则数列{an}的前19项和S19=( )
| A. | 120 | B. | 119 | C. | 114 | D. | 110 |
1.函数f(x)=x3-3x2+2在区间[-1,1]上最大值为M,最小值为m,则M-m的值为( )
| A. | 2 | B. | -4 | C. | 4 | D. | -2 |
 将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:
将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式: