题目内容
15.已知△ABC中,AB=2$\sqrt{3}$,AC+$\sqrt{3}$BC=6,D为AB的中点,当CD取最小值时,△ABC面积为$\frac{3\sqrt{23}}{8}$.分析 根据余弦定理,结合二次函数的图象和性质,可得BC=$\frac{3\sqrt{3}}{2}$时,CD的最小值为$\frac{\sqrt{6}}{2}$,由余弦定理求出cosB,进而求出sinB,代入三角形面积公式,可得答案
解答  解:∵AB=2$\sqrt{3}$,AC+$\sqrt{3}$BC=6,D为AB的中点,
解:∵AB=2$\sqrt{3}$,AC+$\sqrt{3}$BC=6,D为AB的中点,
根据余弦定理可得:AC2=AD2+CD2-2AD•CD•cos∠ADC,且CB2=BD2+CD2-2BD•CD•cos∠CDB,
即(6-$\sqrt{3}$BC)2=3+CD2-2$\sqrt{3}$CD•cos∠ADC,CB2=3+CD2-2$\sqrt{3}$•CD•cos∠CDB,
∵∠CDB=π-∠ADC,
∴(6-$\sqrt{3}$BC)2+CB2=6+2CD2-
∴CD2=2CB2-6$\sqrt{3}$BC+15=2(CB-$\frac{3\sqrt{3}}{2}$)2+$\frac{3}{2}$,
当BC=$\frac{3\sqrt{3}}{2}$时,CD的最小值为$\frac{\sqrt{6}}{2}$,
此时cosB=$\frac{B{C}^{2}+B{D}^{2}-C{D}^{2}}{2•BC•BD}$=$\frac{\frac{27}{4}+3-\frac{6}{4}}{2×\frac{3\sqrt{3}}{2}×\sqrt{3}}$=$\frac{11}{12}$,
∴sinB=$\frac{\sqrt{23}}{12}$,
∴S△ABC=$\frac{1}{2}$×$\frac{3\sqrt{3}}{2}$×2$\sqrt{3}$×$\frac{\sqrt{23}}{12}$=$\frac{3\sqrt{23}}{8}$,
故答案为:$\frac{3\sqrt{23}}{8}$.
点评 本题考查的知识点是余弦定理的应用,三角形面积公式,同角三角函数的基本关系,难度中档

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值的大小及方差的大小(不要求计算出具体值,给出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此2×2列联表,并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关;
| A | B | 合计 | |
| 认可 | |||
| 不认可 | |||
| 合计 |
附:参考数据:
(参考公式:${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$)
| A. | 4 | B. | 17 | C. | 28 | D. | 41 |
| A. | (-∞,0)∪(0,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$) |
| A. | [0,2] | B. | (1,2] | C. | [1,2) | D. | (1,4] |
| A. | ?x0>2,${2^{x_0}}-3≤0$ | B. | ?x≤2,2x-3>0 | C. | ?x>2,2x-3≤0 | D. | ?x0>2,${2^{x_0}}-3>0$ |

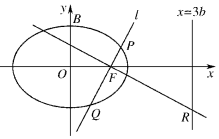 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.