题目内容
5.下列命题中真命题是( )| A. | 若m⊥α,m?β,则α⊥β | |
| B. | 若m?α,n?α,m∥β,n∥β,则α∥β | |
| C. | 若α∩β=m,n∥m,则n∥α且n∥β | |
| D. | 若m?α,n?α,m,n是异面直线,那么n与α相交 |
分析 由面面垂直的判定判断A;举例说明B、C、D错误.
解答 解:若m⊥α,m?β,由面面垂直的判断可得α⊥β,故A是真命题;
若m?α,n?α,m∥β,n∥β,则α∥β,是假命题,当m∥n不一定有α∥β;
若α∩β=m,n∥m,则n∥α且n∥β,是假命题,还有可能是n?α或n?β;
若m?α,n?α,m,n是异面直线,那么n与α相交,是假命题,有可能n∥α.
故选:A.
点评 本题考查命题的真假判断与应用,考查了学生的空间想象能力和思维能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.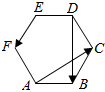 如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )
如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )
 如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )
如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )| A. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | B. | $\frac{1}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$ |
20.函数y=($\frac{1}{2}$)x-log2x的零点为x0,则( )
| A. | x0<1 | B. | x0>3 | C. | 2<x0<3 | D. | 1<x0<2 |
17.以双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的左焦点为圆心,且经过此双曲线右顶点的圆的标准方程为( )
| A. | (x-3)2+y2=25 | B. | (x-3)2+y2=16 | C. | (x+3)2+y2=16 | D. | (x+3)2+y2=25 |