题目内容
18.若一段圆弧的长度等于该圆内接正三角形的边长,则这段弧所对圆心角弧度为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 不妨设等边△ABC的外接圆的半径为2,根据图形所作的辅助线,可求出边长,再根据弧长公式即可求出答案.
解答 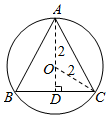 解:不妨设等边△ABC的外接圆的半径为2,取BC的中点D,连接OD,OC,则∠OCB=30°.
解:不妨设等边△ABC的外接圆的半径为2,取BC的中点D,连接OD,OC,则∠OCB=30°.
由垂径定理的推论可知,OD⊥BC,
在Rt△OCD中,OD=$\frac{1}{2}$OC=1,∴CD=$\sqrt{3}$,∴边长BC=2$\sqrt{3}$.
设该圆弧所对圆心角的弧度数为θ,
则由弧长公式可得2θ=2$\sqrt{3}$,
∴θ=$\sqrt{3}$.
故选:C.
点评 本题考查了圆的内接正三角形的边长与半径的关系及弧长公式,理解以上知识和计算方法是解决问题的关键,属于中档题.

练习册系列答案
相关题目