题目内容
9．“n＞m＞0”是方程“mx2+ny2=1表示焦点在x轴上的椭圆”的（ ）| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 方程“mx2+ny2=1表示焦点在x轴上的椭圆”?$\frac{1}{m}＞\frac{1}{n}$＞0?n＞m＞0．即可判断出结论．
解答 解：方程“mx2+ny2=1表示焦点在x轴上的椭圆”?$\frac{1}{m}＞\frac{1}{n}$＞0?n＞m＞0．
“n＞m＞0”是方程“mx2+ny2=1表示焦点在x轴上的椭圆”的充要条件．
故选：C．
点评 本题考查了椭圆的标准方程及其性质、不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
17．
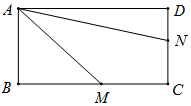如图，某地区有四个公司分别位于矩形ABCD的四个顶点，且AB=1km，BC=2km，四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草，其中M，N分别在直线BC，CD上运动，∠MAN=30°，设∠BAM=α，当三角AMN的面积最小时，此时α=（ ）
如图，某地区有四个公司分别位于矩形ABCD的四个顶点，且AB=1km，BC=2km，四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草，其中M，N分别在直线BC，CD上运动，∠MAN=30°，设∠BAM=α，当三角AMN的面积最小时，此时α=（ ）| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{5π}{12}$ |
4．已知变量x，y满足$\left\{{\begin{array}{l}{1≤x+y≤3}\\{-1≤x-y≤1}\end{array}}\right.$，若目标函数z=2x+y取到最大值a，则（x+$\frac{1}{x}$-2）a的展开式中x2的系数为（ ）
| A． | -144 | B． | -120 | C． | -80 | D． | -60 |
14．已知函数$f（x）=\sqrt{x}sinx$，则f'（π）=（ ）
| A． | $\sqrt{π}$ | B． | $\frac{{\sqrt{π}}}{2π}$ | C． | $-\sqrt{π}$ | D． | $\frac{{\sqrt{2π}}}{2π}$ |
19．已知函数f（x）=kx，g（x）=$\frac{lnx}{x}$，若关于x的方程f（x）=g（x），在区间[$\frac{1}{e}$，e]内有两个实数解，则实数k的取值范围是（ ）
| A． | [$\frac{1}{{e}^{2}}$，$\frac{1}{2e}$） | B． | （$\frac{1}{2e}$，$\frac{1}{e}$] | C． | （0，$\frac{1}{{e}^{2}}$） | D． | （$\frac{1}{e}$，+∞） |