题目内容
17．（1）化简$\sqrt{1-si{n}^{2}100°}$；（2）用tanα表示$\frac{sinα+cosα}{2sinα-cosα}$，sin2α+sinαcosα+3cos2α
分析 原式分母看做“1”，利用同角三角函数间的基本关系化简．
解答 解：（1）$\sqrt{1-si{n}^{2}100°}$=$\sqrt{1-si{n}^{2}80}$=cos80，
（2）$\frac{sinα+cosα}{2sinα-cosα}$=$\frac{tanα+1}{2tanα-1}$，
sin2α+sinαcosα+3cos2α=$\frac{si{n}^{2}α+sinαcosα+3co{s}^{2}α}{si{n}^{2}α+co{s}^{2}α}$=$\frac{ta{n}^{2}α+tanα+3}{1+ta{n}^{2}α}$．
点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
12．
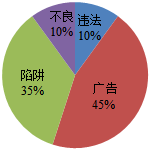2014年春晚唱响的一曲“群发的我不回”让短信再次成为关注焦点，手机短信中不乏大量垃圾短信，垃圾短信一般分为不良短信、广告短信、违法短信、陷阱短信等四类，其分布如图．
将频率作为概率，解决下列问题：
（1）在这些人中任取一位，接到的垃圾短信低于15条的概率是多少？
（2）估计垃圾短信条数不低于20条的人中每人在一月内接到的广告短信的条数；
（3）为进一步了解这些垃圾短信的分类信息，再从条数在[25，30）中的人甲、乙中选出1位，从条数在[20，25）中的人丙、丁、戊、己、庚中选出2位进行试验研究，求甲和丁同时被选到的概率．
2014年春晚唱响的一曲“群发的我不回”让短信再次成为关注焦点，手机短信中不乏大量垃圾短信，垃圾短信一般分为不良短信、广告短信、违法短信、陷阱短信等四类，其分布如图．| 条数 | [0，5） | [5，10） | [10，15） | [15，20） | [20，25） | [25，30） |
| 人数 | 1 | 2 | 5 | 9 | 5 | 2 |
（1）在这些人中任取一位，接到的垃圾短信低于15条的概率是多少？
（2）估计垃圾短信条数不低于20条的人中每人在一月内接到的广告短信的条数；
（3）为进一步了解这些垃圾短信的分类信息，再从条数在[25，30）中的人甲、乙中选出1位，从条数在[20，25）中的人丙、丁、戊、己、庚中选出2位进行试验研究，求甲和丁同时被选到的概率．