题目内容
设函数f(x)=(x2-x-1)e-x.
(1)求f(x)的单调区间和极值;
(2)关于x的方程f(x)=a在区间[-1,4]上有两个根,求a的取值范围.
(1)求f(x)的单调区间和极值;
(2)关于x的方程f(x)=a在区间[-1,4]上有两个根,求a的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)先求出函数的导数,令f′(x)=0,从而得到函数的单调区间和极值;(2)由题知,只需要函数y=f(x) 和函数y=a 的图象有两个交点即可.
解答:
解:(1)f'(x)=-x(x-3)e-x,由f'(x)=0,解得x=0或3,
则x,f′(x),f(x)的变化情况如下表:
由上表得,f(x)的单调增区间为(0,3),单调减区间为(-∞,0),(3,+∞);
当x=0时f(x)有极小值-1,当x=3时,f(x)有极大值5e-3.
(2)由题知,只需要函数y=f(x) 和函数y=a 的图象有两个交点即可.
∵(f(-1)=e,f(4)=11e-4,
∴f(-1)>f(3)>f(4)>f(0)
由(1)知f(x)在,当[-1,0)上单调递减,(0,3)上单调递增,在(3,4]在上单调递减.
∴当a=5e-3或-1<a<11e-4时,y=f(x) 和y=a 的图象有两个交点.
即方程f(x)=a在区间[-1,4]上有两个根.
则x,f′(x),f(x)的变化情况如下表:
| x | (-∞,0) | 0 | (0,3) | 3 | (3,+∞) |
| f’(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | 极小值-1 | ↗ | 极大值5e-3 | ↘ |
当x=0时f(x)有极小值-1,当x=3时,f(x)有极大值5e-3.
(2)由题知,只需要函数y=f(x) 和函数y=a 的图象有两个交点即可.
∵(f(-1)=e,f(4)=11e-4,
∴f(-1)>f(3)>f(4)>f(0)
由(1)知f(x)在,当[-1,0)上单调递减,(0,3)上单调递增,在(3,4]在上单调递减.
∴当a=5e-3或-1<a<11e-4时,y=f(x) 和y=a 的图象有两个交点.
即方程f(x)=a在区间[-1,4]上有两个根.
点评:本题考察了利用导数研究函数的单调性,函数的极值问题,本题渗透了转化思想,是一道基础题.

练习册系列答案
相关题目
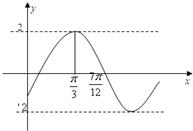 已知函数y=Asin(ωx+φ)(ω>0,A>0,|φ|<
已知函数y=Asin(ωx+φ)(ω>0,A>0,|φ|<| π |
| 2 |
A、y=sin(2x+
| ||
B、y=2sin(x-
| ||
C、y=2sin(2x-
| ||
D、y=2sin(2x+
|
直线2x-y+1=0与圆x2+y2-2mx-4my+m2-1=0的位置关系是( )
| A、相交但不过圆心 |
| B、相交且肯定过圆心 |
| C、相交或相切 |
| D、相交或相切或. |