题目内容
已知定义在R上的函数f(x)=-2x3+bx2+cx(b,c∈R),函数F(x)=f(x)-3x2是奇函数,函数f(x)满足f′(-1)=0.
(1)求f(x)的解析式;
(2)讨论f(x)在区间(-3,3)上的单调性.
(1)求f(x)的解析式;
(2)讨论f(x)在区间(-3,3)上的单调性.
考点:利用导数研究函数的单调性,函数解析式的求解及常用方法
专题:导数的综合应用
分析:(1)根据函数的奇偶性和导数公式,求出b,c的值,即可求f(x)的解析式;
(2)求出函数的导数,利用导数和单调性之间的关系,即可得到(x)在区间(-3,3)上的单调性.
(2)求出函数的导数,利用导数和单调性之间的关系,即可得到(x)在区间(-3,3)上的单调性.
解答:
解:(1)∵f(x)=-2x3+bx2+cx,
∴f'(x)=-6x2+2bx+c.
F(x)=f(x)-3x2是奇函数,得b=3,
f'(-1)=-6-2b+c=0,得c=12,
∴f(x)-2x3+3x2+12.
(2)令f'(x)=-6x2+6x+12=0得x=2或-1
∴单调递增区间为(-1,2),单调递减区间为(-3,-1),(2,3).
∴f'(x)=-6x2+2bx+c.
F(x)=f(x)-3x2是奇函数,得b=3,
f'(-1)=-6-2b+c=0,得c=12,
∴f(x)-2x3+3x2+12.
(2)令f'(x)=-6x2+6x+12=0得x=2或-1
| x | (-3,-1) | -1 | (-1,2) | 2 | (2,3) |
| f′(x) | - | 0 | + | 0 | - |
点评:本题主要考查函数解析式和函数单调性的判断,求函数的导数,利用函数单调性和导数之间的关系是解决本题的关键.

练习册系列答案
相关题目
下列函数中,在[1,+∞)上为增函数的是( )
| A、y=(x-2)2 | ||
| B、y=|x-1| | ||
C、y=
| ||
| D、y=-(x+1)2 |
 执行如图所示的程序框图,如果输入a=2,b=2,那么输出的a值为( )
执行如图所示的程序框图,如果输入a=2,b=2,那么输出的a值为( )| A、log316 |
| B、256 |
| C、16 |
| D、4 |
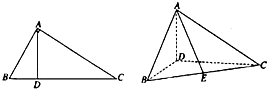 如图,在△ABC中,AB⊥AC,AD⊥BC,∠ABC=
如图,在△ABC中,AB⊥AC,AD⊥BC,∠ABC=