题目内容
数列{an}中,满足a2=4,a3=6,其前n项和Sn满足Sn=an2+bn(a,b∈R).
(1)求实数a,b的值,并求数列{an}的通项公式;
(2)若数列{
+bn}是首项为a,公比为2b的等比数列,求数列{bn}的前n项和Tn.
(1)求实数a,b的值,并求数列{an}的通项公式;
(2)若数列{
| 1 |
| Sn |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由a2=4,a3=6,其前n项和Sn满足Sn=an2+bn,利用公式an=
列出方程组能求出a=1,b=1,从而Sn=n2+n,再由公式an=
能求出an=2n.
(2)由已知得
+bn=2n-1,从而bn=2n-1+
-
,由此利用分组求和法和裂项求和法能求出数列{bn}的前n项和Tn.
|
|
(2)由已知得
| 1 |
| n2+n |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(1)∵数列{an}中,满足a2=4,a3=6,其前n项和Sn满足Sn=an2+bn(a,b∈R),
∴
,
解得a=1,b=1,∴Sn=n2+n,
∴a1=S1=1+1=2,
n≥2时,an=Sn-Sn-1=(n2+n)-[(n-1)2+(n-1)]=2n,
当n=1时,上式成立,
∴an=2n.
(2)∵数列{
+bn}是首项为a,公比为2b的等比数列,
∴
+bn=2n-1,∴bn=2n-1+
-
,
∴Tn=(1+2+22+23+…+2n-1)+(1-
+
-
+…+
-
)
=
+(1-
)
=2n-
.
∴
|
解得a=1,b=1,∴Sn=n2+n,
∴a1=S1=1+1=2,
n≥2时,an=Sn-Sn-1=(n2+n)-[(n-1)2+(n-1)]=2n,
当n=1时,上式成立,
∴an=2n.
(2)∵数列{
| 1 |
| Sn |
∴
| 1 |
| n2+n |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=(1+2+22+23+…+2n-1)+(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1-2n |
| 1-2 |
| 1 |
| n+1 |
=2n-
| 1 |
| n+1 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要注意分组求和法和裂项求和法的合理运用.

练习册系列答案
相关题目
函数y=x(|x|-1)的图象是( )
A、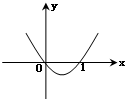 |
B、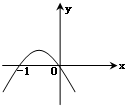 |
C、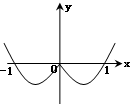 |
D、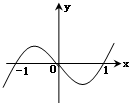 |
与椭圆
+
=1共焦点,离心率互为倒数的双曲线方程是( )
| x2 |
| 16 |
| y2 |
| 12 |
A、x2-
| ||||
B、
| ||||
C、
| ||||
D、
|
已知a=2-
,b=log2
,c=log23,则( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、c>a>b |
| B、a>c>b |
| C、c>b>a |
| D、a>b>c |
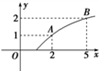 已知函数f(x)=log3(ax+b)的部分图象如图所示.
已知函数f(x)=log3(ax+b)的部分图象如图所示.