题目内容
12.(1)求函数f(x)=cos2x-sinx的最大值;(2)求函数f(x)=cos2x-asinx的最小值.(用含a的代数式表示)
分析 (1)利用三角函数的平方关系式,通过二次函数的最值求解即可.
(2)利用二次函数的最值,通过a的范围的讨论,求解函数的最值即可.
解答 解:(1)f(x)=1-sin2x-sinx=$-{(sinx+\frac{1}{2})^2}+\frac{5}{4}$,
∵sinx∈[-1,1],∴f(x)的最大值为$\frac{5}{4}$.
(2)f(x)=1-sin2x-asinx=$-{(sinx+\frac{a}{2})^2}+1+\frac{a^2}{4}$,
∵sinx∈[-1,1],
当a≤0时,f(x)的最小值为a,
当a>0时,f(x)的最小值为-a.
点评 本题考查函数的最值的求法,二次函数的简单性质以及三角函数的最值的应用,考查分类讨论思想的应用.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
3.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,过F2的直线与椭圆交于A、B两点,若△F1AB是等边三角形,则离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{3}{4}$ |
20.若两点的坐标是A(3cosα,3sinα,1),B(2cosβ,2sinβ,1),则|AB|的取值范围是( )
| A. | [0,5] | B. | [1,5] | C. | (0,5) | D. | [1,25] |
17.设函数f(x)=ex,g(x)=lnx-2.
(Ⅰ)证明:$g(x)≥-\frac{e}{x}$;
(Ⅱ)若对所有的x≥0,都有$f(x)-\frac{1}{f(x)}≥ax$,求实数a的取值范围.
(Ⅰ)证明:$g(x)≥-\frac{e}{x}$;
(Ⅱ)若对所有的x≥0,都有$f(x)-\frac{1}{f(x)}≥ax$,求实数a的取值范围.
1.设实数a=log23,b=log${\;}_{\frac{1}{3}}$$\frac{1}{2}$,c=$\frac{1}{{∫}_{0}^{π}xdx}$,则( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
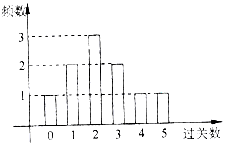 某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.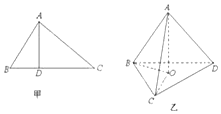 如图甲,在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.如图乙,在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,探究S△ABC、S△BCO、S△BCD这三者之间满足的关是S△ABC2=S△BCO•S△BCD.
如图甲,在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.如图乙,在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,探究S△ABC、S△BCO、S△BCD这三者之间满足的关是S△ABC2=S△BCO•S△BCD.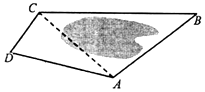 如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD的各边的AB=5,BC=8,CD=3,DA=5长度(单位:km):,如图所示,若A、B、C、D四点共圆.
如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD的各边的AB=5,BC=8,CD=3,DA=5长度(单位:km):,如图所示,若A、B、C、D四点共圆.