题目内容
4.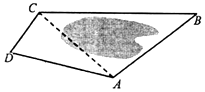 如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD的各边的AB=5,BC=8,CD=3,DA=5长度(单位:km):,如图所示,若A、B、C、D四点共圆.
如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD的各边的AB=5,BC=8,CD=3,DA=5长度(单位:km):,如图所示,若A、B、C、D四点共圆.求:线段AC的长和△ABC的面积.
分析 利用余弦定理,结合∠B+∠D=π,即可求出AC的长,再用余弦定理即可求出B的大小,根据三角形的面积公式即可求出答案
解答 解:∵A、B、C、D四点共圆,圆内接四边形的对角和为π.
∴∠B+∠D=π,
∴由余弦定理可得AC2=52+32-2•5•3•cosD=34-30cosD,
AC2=52+82-2•5•8•cosB=89-80cosB,
∵∠B+∠D=π,即cosB=-cosD,
∴-$\frac{34-A{C}^{2}}{30}$=$\frac{89-A{C}^{2}}{80}$,
∴可解得AC=7.
由余弦定理可得cosB=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•BC}$=$\frac{25+64-49}{2×5×8}$=$\frac{1}{2}$,
∴B=60°,
∴S△ABC=$\frac{1}{2}$•BC•|$\overrightarrow{AB}$|•sinB=$\frac{1}{2}$×8×5×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$.
点评 本题考查余弦定理,考查三角函数知识,正确运用余弦定理是关键,属于中档题

练习册系列答案
相关题目
19.对变量X与Y的卡方统计量Χ2的值,说法正确的是( )
| A. | Χ2越大,“X与Y有关系”可信程度越小 | |
| B. | Χ2越小,“X与Y有关系”可信程度越小 | |
| C. | Χ2越接近0,“X与Y无关”程度越小 | |
| D. | Χ2越大,“X与Y无关”程度越大 |
9.直线y=x+b与曲线$\left\{\begin{array}{l}{x=\frac{3}{2}cosθ}\\{y=\frac{3}{2}sinθ}\end{array}\right.$(θ为参数,且-$\frac{π}{2}$≤θ≤$\frac{π}{2}$)有两个不同的交点,则实数b的取值范围是( )
| A. | (-$\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$) | B. | (-$\frac{3\sqrt{2}}{2}$,-$\frac{3}{2}$] | C. | (-$\sqrt{2}$,$\sqrt{2}$) | D. | (-$\sqrt{2}$,-1] |