题目内容
1.已知函数f(x)=xex-5.(1)试求函数f(x)的单调区间及最值
(2)设函数g(x)=|f(x-3)+5|,若方程[g(x)]2+tg(x)+1=0(t∈R)有四个实数根,求t的取值范围.
分析 (1)f′(x)=ex(x+1),利用导数判断出f(x)在(-∞,-1)上为减函数;在(-1,+∞)上为增函数,$f(x)≥f(-1)=-\frac{1}{e},所以f{(x)_{min}}=-\frac{1}{e}$
(2)画出g(x)=|(x-3)ex-3|的图象,方程有四个实数根问题可结合图象解决.$结合图象令g(x)=u,问题转化为F(u)={u^2}+tu+1在区间(0,\frac{1}{e})与(\frac{1}{e},+∞)$上各有一个零点,由题意F(0)>0$\left\{\begin{array}{l}F(0)>0\\ F(\frac{1}{e})<0\end{array}\right.⇒t<-\frac{{{e^2}+1}}{e}$
解答 解:(1)∵函数f(x)=xex-5.
∴f′(x)=ex(x+1),f′(x)=ex(x+1)=0,x=-1,
f′(x)=ex(x+1)>0,x>-1,
f′(x)=ex(x+1)<0,x<-1,
∴f(x)在(-∞,-1)上为减函数;在(-1,+∞)上为增函数,
$f(x)≥f(-1)=-\frac{1}{e},所以f{(x)_{min}}=-\frac{1}{e}$,
(2)g(x)=|(x-3)ex-3|的图象,
方程有四个实数根问题可结合图象解决.
$结合图象令g(x)=u,问题转化为F(u)={u^2}+tu+1在区间(0,\frac{1}{e})与(\frac{1}{e},+∞)$
上各有一个零点,由题意F(0)>0$\left\{\begin{array}{l}F(0)>0\\ F(\frac{1}{e})<0\end{array}\right.⇒t<-\frac{{{e^2}+1}}{e}$.
点评 本题中考查了函数的性质,数形结合的思想,不等式的运用,属于综合题目,学生要有一定的综合能力.

 已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形,又PD⊥底面ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形,又PD⊥底面ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.(Ⅰ)证明:DN∥平面PMB;
(Ⅱ)求二面角P-AB-D的余弦值.
| A. | $\frac{{3}^{2015}}{2}$+$\frac{3}{2}$ | B. | $\frac{{3}^{2015}}{8}$ | C. | $\frac{{3}^{2015}}{8}$+$\frac{3}{2}$ | D. | $\frac{{3}^{2015}}{2}$ |
| A. | (1,2) | B. | (0,1) | C. | (-2,-1) | D. | (-1,0) |
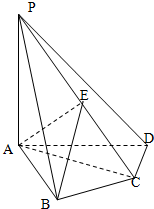 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.