题目内容
20.关于函数f(x)=$\sqrt{3}$cos(2x+$\frac{π}{6}$),x∈R,下列结论中正确的个数是( )①若f(x1)=f(x2),则x1-x2必是π的整数倍;
②函数f(x)的图象关于直线x=$\frac{5π}{12}$对称;
③函数f(x)在区间[0,$\frac{π}{2}$]上的值域为[-$\frac{3}{2},\frac{3}{2}$];
④函数f(x)的解析式可写为f(x)=$\sqrt{3}sin(2x+\frac{2π}{3})$.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 根据三角函数的图象关系、对称性进行判断.
解答 解:①由题意,函数的周期为π,∴若f(x1)=f(x2),则x1-x2必是π的整数倍,正确;
②x=$\frac{5π}{12}$时,f(x)=$\sqrt{3}$cos(2x+$\frac{π}{6}$)=-$\sqrt{3}$,∴函数f(x)的图象关于直线x=$\frac{5π}{12}$对称,正确;
③在区间[0,$\frac{π}{2}$]上,2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],函数f(x)在区间[0,$\frac{π}{2}$]上的值域为[-$\frac{3}{2}$-$\sqrt{3}$],不正确;
④函数f(x)的解析式可写为f(x)=$\sqrt{3}$cos(2x+$\frac{π}{6}$)=$\sqrt{3}$sin(2x+$\frac{π}{6}$+$\frac{π}{2}$)=$\sqrt{3}sin(2x+\frac{2π}{3})$,正确.
故选B.
点评 本题主要考查与三角函数有关的图象和性质,根据三角函数的对称性是解决本题的关键.

练习册系列答案
相关题目
8.长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,则异面直线BC1与AC所成角的余弦值为( )
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{1}{2}$ |
12. 已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形,又PD⊥底面ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形,又PD⊥底面ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
(Ⅰ)证明:DN∥平面PMB;
(Ⅱ)求二面角P-AB-D的余弦值.
 已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形,又PD⊥底面ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形,又PD⊥底面ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.(Ⅰ)证明:DN∥平面PMB;
(Ⅱ)求二面角P-AB-D的余弦值.
9.已知数列{an}满足:a1=$\frac{3}{8}$,an+2-an≤3n,an+6-an≥91•3n,则a2015=( )
| A. | $\frac{{3}^{2015}}{2}$+$\frac{3}{2}$ | B. | $\frac{{3}^{2015}}{8}$ | C. | $\frac{{3}^{2015}}{8}$+$\frac{3}{2}$ | D. | $\frac{{3}^{2015}}{2}$ |
10.函数f(x)=x3-x+2在下列区间内一定存在零点的是( )
| A. | (1,2) | B. | (0,1) | C. | (-2,-1) | D. | (-1,0) |
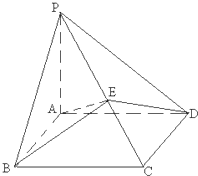 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=$\sqrt{2}$,∠ABC=45°,AE⊥PC,垂足为E.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=$\sqrt{2}$,∠ABC=45°,AE⊥PC,垂足为E.