题目内容
2.已知x,y满足$\left\{\begin{array}{l}{y≤x}\\{x+2y≤4}\\{y≥-2}\end{array}\right.$,则目标函数z=x2+y2+2x-2y+2的最小值为22.分析 由约束条件作出可行域,把给出的目标函数配方,然后利用其几何意义得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{y≤x}\\{x+2y≤4}\\{y≥-2}\end{array}\right.$作出可行域如图,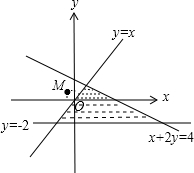
z=x2+y2+2x-2y+2=(x+1)2+(y-1)2,
其几何意义为可行域内的动点与定点M(-1,1)距离的平方,
其最小值为$|{OM|}^{2}=(\sqrt{2})^{2}=2$.
故答案为:2.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
1.已知定义域为R的偶函数f(x)满足对任意x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数f(x)与函数g(x)=loga(|x|+2)在(0,+∞)上至少有三个交点,则实数a的取值范围是( )
| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{\sqrt{5}}{5}$) | D. | (0,$\frac{\sqrt{6}}{6}$) |
11.命题“?x∈(1,+∞),2x>2”的否定是( )
| A. | ?x0∈(-∞,1],${2^{x_0}}$≤2 | B. | ?x0∈(1,+∞),${2^{x_0}}$≤2 | ||
| C. | ?x∈(-∞,1],2x≤2 | D. | ?x∈(1,+∞),2x<2 |
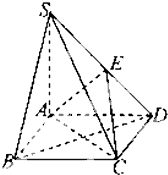 如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$.
如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$.