题目内容
1.已知定义域为R的偶函数f(x)满足对任意x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数f(x)与函数g(x)=loga(|x|+2)在(0,+∞)上至少有三个交点,则实数a的取值范围是( )| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{\sqrt{5}}{5}$) | D. | (0,$\frac{\sqrt{6}}{6}$) |
分析 根据定义域为R的偶函数f(x)满足对?x∈R,有f(x+2)=f(x)-f(1),可以令x=-1,求出f(1),再求出函数f(x)的周期为2,当x∈[2,3]时,f(x)=-2x2+12x-18,画出图形,根据函数f(x)与函数g(x)=loga(|x|+2)在(0,+∞)上至少有三个交点,利用数形结合的方法进行求解;
解答 解:因为 f(x+2)=f(x)-f(1),且f(x)是定义域为R的偶函数,
令x=-1 所以 f(-1+2)=f(-1)-f(1),f(-1)=f(1),
即 f(1)=0 则有,f(x+2)=f(x),
f(x)是周期为2的偶函数,
当x∈[2,3]时,f(x)=-2x2+12x-18=-2(x-3)2,
图象为开口向下,顶点为(3,0)的抛物线,
∵函数f(x)与函数g(x)=loga(|x|+2)在(0,+∞)上至少有三个交点,
∵f(x)≤0,
∴g(x)≤0,可得a<1,
要使函数f(x)与函数g(x)=loga(|x|+2)在(0,+∞)上至少有三个交点,
如图要求g(2)>f(2),可得: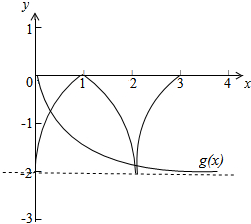
就必须有 loga(2+2)>f(2)=-2,
∴可得loga4>-2,∴解得-$\frac{1}{2}$<a<$\frac{1}{2}$又a>0,
∴0<a<$\frac{1}{2}$,
故选:B.
点评 此题主要考查函数周期性及其应用,解题的过程中用到了数形结合的方法,这也是高考常考的热点问题,此题是一道中档题.

练习册系列答案
相关题目
12.若f(x)=5-3x(2<x≤4),则f(x)的值域为( )
| A. | R | B. | [-7,-1) | C. | (-7,-1] | D. | {-7,-1} |
9.数列{1+2n-1}的前n项的和为( )
| A. | 1+2n | B. | 2+2n | C. | n+2n-1 | D. | n+2+2n |
6.利用计算机在区间(0,1)上产生两个随机数a和b,则关于x的方程x2+2ax+b=0有实根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |