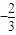题目内容
设sinα+sinβ=
，cosα+cosβ=
，求cos（α-β）的值．
| 1 |
| 2 |
| 1 |
| 3 |
∵sinα+sinβ=
，cosα+cosβ=
，分别平方得
sin2α+sin2β+2sinαsinβ=
，cos2α+cos2β+2cosαcosβ=
，两式相加得
2+2sinαsinβ+2cosαcosβ=
∴sinαsinβ+cosαcosβ=cos（α-β）=-
；
| 1 |
| 2 |
| 1 |
| 3 |
sin2α+sin2β+2sinαsinβ=
| 1 |
| 4 |
| 1 |
| 9 |
2+2sinαsinβ+2cosαcosβ=
| 13 |
| 36 |
∴sinαsinβ+cosαcosβ=cos（α-β）=-
| 59 |
| 72 |
练习册系列答案
相关题目
,则sinα-cos2β的最大值为( )
B．
C．-
D．-
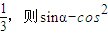β，的最大值为（ ）
